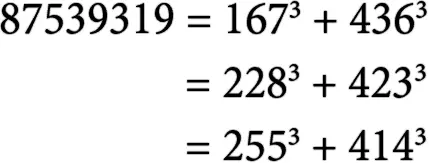Саймон Сингх - Симпсоны и их математические секреты

Рамануджан добился многочисленных, сложных и блестящих достижений, а его гениальность получила признание в 1918 году, когда он был избран самым молодым членом Королевского общества. Переезд в Кембридж позволил разуму Рамануджана пережить невероятный расцвет, а вот суровая английская зима и изменение рациона питания негативно сказались на его здоровье. В конце 1918 года Рамануджан покинул Кембридж и лег в частную лечебницу Colinette House в пригороде Лондона Патни. Именно в этих условиях и состоялась та самая беседа, которая связывает Рамануджана с «Футурамой».

Вот что говорил об этом Харди: «Помню, как я однажды отправился проведать его в Патни. Я приехал на такси с номером 1729 и заметил, что это число кажется мне довольно скучным и что я надеюсь, в нем нет никакого плохого предзнаменования. “Нет, – ответил он, – это очень интересное число; это наименьшее число, которое можно представить в виде суммы кубов двумя разными способами”».

Эти двое явно не относились к любителям светской болтовни и сплетен. Как всегда, их разговор был посвящен числам, а его суть можно выразить так:

1729 = 1³ + 12³ = 9³ + 10³

Другими словами, если бы у нас было 1729 маленьких кубиков, мы могли бы сложить их в виде двух кубов со сторонами 1 × 1 × 1 и 12 × 12 × 12 или 9 × 9 × 9 и 10 × 10 × 10. Только немногие числа можно разделить на два куба, и еще меньше чисел, которые можно разделить на два куба двумя разными способами…, а число 1729 – минимальное число с таким свойством. В честь комментария Рамануджана по поводу номера такси, в котором ехал Харди, в математических кругах это число принято называть «числом такси» .

Импровизированное замечание Рамануджана пробудило у математиков такой интерес, что они поставили вопрос несколько иначе: чему равно минимальное число, которое можно представить в виде суммы двух кубов тремя разными способами? Ответ – 87 539 319, поскольку:

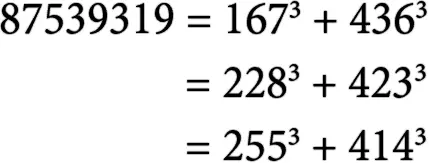
Это число, которое тоже называют числом такси, присутствует в полнометражном мультфильме «Большой куш Бендера» (Bender’s Big Score, 2007 год). Когда Фрай вызывает такси, на его крыше красуется номер 87 539 319. Безусловно, это вполне естественно, когда в качестве номера такси (в обычном смысле) выступает число такси (в математическом смысле).

Таким образом, неоднократно упоминая число 1729 в эпизодах «Футурамы», а также включив в один из эпизодов число 87 539 319, сценаристы мультсериала отдают дань уважения Рамануджану, история которого мало кому известна за пределами мира математики. Эта вдохновляющая история о гениальном человеке, который стал знаменитым благодаря преподавателю Кембриджского университета, увы, имеет трагический конец. В 1919 году Рамануджан, страдавший от различных болезней, в том числе от авитаминоза и туберкулеза, вернулся в Индию в надежде, что более теплый климат и привычная вегетарианская диета помогут ему восстановить здоровье. Однако, прожив в Индии около года, 26 апреля 1920 года он умер в возрасте тридцати двух лет.

Тем не менее идеи Рамануджана до сих пор остаются и навсегда останутся в самом сердце современной математики. Отчасти это объясняется универсальностью языка математики, а отчасти абсолютным характером математических доказательств. В отличие от идей в области искусства и гуманитарных наук, математические теоремы никогда не выходят из моды. Сам Харди сказал об этом следующее: «Архимеда будут помнить даже тогда, когда Эсхила забудут, потому что языки умирают, а математические идеи бессмертны. Возможно, “бессмертие” – глупое слово, но, по всей вероятности, математик имеет на него наибольшие шансы, что бы оно ни означало».

Присутствующие в «Футураме» ссылки на числа такси можно связать с Кеном Килером, которого считают одним из самых математически одаренных сценаристов как «Симпсонов», так и «Футурамы». По словами самого Килера, его увлеченность математикой сформировалась под влиянием отца, Мартина Килера – врача, любившего играть с числами. Каждый раз, когда они всей семьей ходили в ресторан и получали счет в конце ужина, отец искал в этом чеке простые числа и предлагал детям присоединиться к поискам. Кен Килер помнит, как когда-то он спросил отца, существует ли быстрый способ сложения квадратов целых чисел. Например, чему равна сумма квадратов первых пяти чисел, или первых десяти чисел, или первых n чисел? Доктор Килер подумал немного, а затем дал совершенно правильный ответ в виде формулы: n³/3 + n ²/2 + n /6. Формулу доктора Килера можно проверить с помощью примера, скажем, когда n = 5: