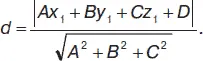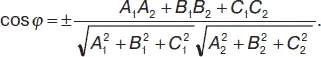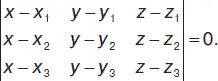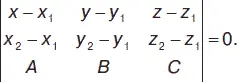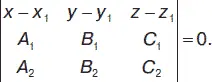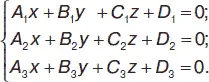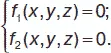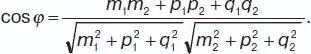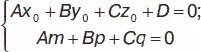Аурика Луковкина - Высшая математика. Шпаргалка

Всякая поверхность в пространстве определяется уравнением вида f ( x, y, z ) = 0.

Общее уравнение плоскости: Ах + Ву + Сz + D = 0. Если А, В, С, D не равны нулю, то уравнение называется полным.

При D = 0 уравнение Ах + Ву + Сz = 0 определяет плоскость, проходящую через начало координат.

Если А = 0, то уравнение определяет плоскость, параллельную оси Ох . Если два из коэффициентов А, В, С равны нулю одновременно, то уравнение определяет плоскость, параллельную одной из координатных плоскостей: при А = 0 и В = 0 параллельно плоскости хОу , при А = 0 и С = 0 параллельно хОz , при В = 0 и С = 0 параллельно yOz . Уравнение Cz = 0 определяет плоскость xOy, By = 0 – плоскость xOz, Ax = 0 – плоскость yOz . Уравнение плоскости в «отрезках»: х / а + у / b + z / c = 1. Расстояние от точки М ( х 1, у 1, z 1) до плоскости:

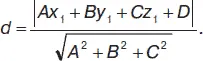
Пусть имеются две плоскости А 1 х + В 1 у + С 1 z + D 1= 0 и А 2 х + В 2 у + С 2 z + D 2= 0. Угол φ между этими плоскостями:

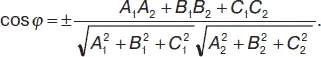
Условие равенства двух плоскостей: А 1 / А 2= В 1 / В 2= С 1 / С 2= D 1 / D 2. Условие параллельности плоскостей: А 1/ А 2= В 1/ В 2= С 1/ С 2. Условие перпендикулярности плоскостей: А 1 А 2+ В 1 В 2+ С 1 С 2= 0. Уравнение плоскости, проходящей через заданную точку М ( х 1, у 1, z 1) параллельно плоскости, заданной уравнением Ах + Ву + Сz + D = 0: А ( х – x 1) + В ( у – y 1) + С ( z – z 1) + D = 0. Уравнение плоскости, проходящей через три точки М 1( х 1, у 1, z 1), М 2( х 2, у 2, z 2), М 3( х 3, у 3, z 3):

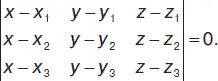
Уравнение плоскости, проходящей через две точки М 1( х 1, у 1, z 1) и М 2( х 2, у 2, z 2) перпендикулярно к плоскости, заданной уравнением A x + B y + C z + D = 0:

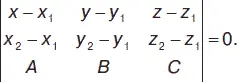
Уравнение плоскости, проходящей через точку М 1( х 1, у 1, z 1) перпендикулярно двум непараллельным плоскостям А 1 х + В 1 у + С 1 z + D 1= 0 и А 2 х + В 2 у + С 2 z + D 2= 0, имеет вид:

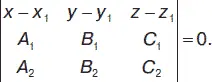
Имеем три плоскости, заданные общими уравнениями:

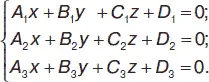
Всякая прямая определяется в пространстве системой двух уравнений

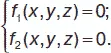
Канонические (симметричные) уравнения прямой:( x – x 0) / m = ( y – y 0) / p = ( z – z 0) / q , прямая проходит через точку M 0( x 0, y 0, z 0). Угол φ между двумя прямыми, заданными каноническими уравнениями:

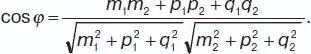
Условие параллельности двух прямых: m 1 / m 2= p 1 / p 2= q 1 / q 2. Условие перпендикулярности двух прямых: m 1 m 2+ p 1 p 2+ q 1 q 2= 0.

Пусть имеются прямая ( x – x 0) / m = ( y – y 0) / p = ( z – z 0) / q и плоскость Ах + Ву + Сz + D = 0. Условие параллельности прямой и плоскости: Am + Bp + Cq = 0. Условие перпендикулярности прямой и плоскости: A / m = B / p = C / q . Условие принадлежности прямой плоскости:

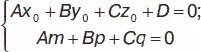
Если прямая задана параметрически x

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.