Аурика Луковкина - Высшая математика. Шпаргалка

При переносе начала координатсправедливо следующее правило: старая координата точки равна новой, сложенной с координатой нового начала в старой системе. Например, если старые координаты точки М были х, у , а координаты нового начала в старой системе О *(х 0, у 0), то координаты точки М в новой системе координат с началом в точке О * будут равны х – х 0, у – у 0т. е. справедливо следующее х = х * + х 0, у = у * + у 0или х * = х – х 0, у * = у – у 0(* новые координаты точки).

При повороте осейна некоторый угол φ справедливы следующие формулы (где х, у – старые координаты точки; х *, у * – новые координаты этой же точки):

x = x * cos α – y * sin α ;

y = x * sin α + y * cos α

или

x * = x cos α + y sin α ;

y * = – x sin α + y cos α .

Линия L , представленная в декартовой системе уравнением n –степени называется алгебраической линией n –порядка.

Окружностьс радиусом R и центром в начале координат описывается уравнением: х 2+ у 2= R 2, если центром окружности является некоторая точка С (а, b ), то уравнением:

( х – а ) 2+ ( у – b ) 2= R 2.

Чтобы уравнение Ах 2+ Вх + Ау 2+ Су + D = 0 описывало окружность, необходимо, чтобы оно не содержало члена с произведением ху , чтобы коэффициенты при х 2и у 2были равны, чтобы В 2+ С 2– 4 АD > 0 (при невыполнении данного неравенства уравнение не представляет никакой линии).

Координаты центра окружности, описанной уравнением Ах 2+ Вх + Ау 2+ Су + D = 0 и ее радиус: a = – B / 2 A, b = – C / 2 A, R 2= ( В 2+ С 2– 4 АD ) / 4 A 2.

Эллипс –сжатая окружность (рис. 3).

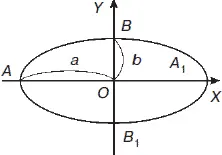
Рис. 3

Прямая АА 1называется осью сжатия, отрезок АА 1= 2 а – большой осью эллипса,отрезок ВВ 1= 2 b – малой осью эллипса( a > b ) точка О – центром эллипса, точки А, А 1, В, В 1– вершинами эллипса. Отношение k = b / a коэффициент сжатиявеличина α = 1 – k = ( a – b ) / a – сжатие эллипса. Эллипс обладает симметрией относительно большой и малой осей и относительно своего центра.

Каноническое уравнение эллипса: x 2/ a 2+ y 2/ b 2= 1.

Другое определение эллипса:эллипс есть геометрическое место точек ( М ), сумма расстояний которых до двух данных точек F, F 1имеет одно и то же значение 2 а ( F 1 M + FM = 2 a ) (рис. 4).

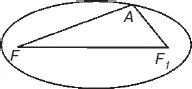
Рис. 4

Точки F и F 1называются фокусами эллипса, а отрезок FF 1– фокусным расстоянием, обозначается FF 1= 2 с , причем с < а . Эксцентриситет эллипса ε – это отношение фокусного расстояния к большой оси ε = с / а . Эксцентриситет эллипса меньше единицы, имеем: k 2= 1 – ε 2.

Гипербола– это геометрическое место точек, разность расстояний которых до двух данных точек F, F 1имеет одно и то же абсолютное значение (рис. 5). | F 1 M – FM | = 2 a . Точки F, F 1называются фокусами гиперболы, расстояние FF 1= 2 c – фокусным расстоянием. Справедливо: c > a .

Каноническое уравнение гиперболы: х 2/ а 2+ у 2/ ( а 2– с 2) = 1. Асимптоты гиперболы заданы уравнениями у = bx / a и y = – bx / a ( b 2= c 2– a 2).

Парабола –это геометрическое место точек равноудаленных от данной точки F (фокуса параболы)и данной прямой PQ (директрисы параболы). Расстояние от фокуса до директрисы FC называется параметром параболыи обозначается р . Вершина параболы – точка О . Каноническое уравнение параболы: у 2= 2 рх .

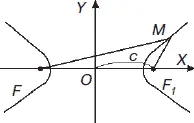
Рис. 5