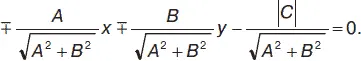Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М , описывается уравнением А ( х – х 1) + В ( у – у 1) = 0.
Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М :
у – у 1= –( х – х 1) / а
или
а ( у – у 1) = х 1– х .
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М ( х 1, у 1), описывается уравнением А ( у – у 1) – В ( х – х 1) = 0.
4. Пусть даны две точки А 1( х 1, у 1), А 2( х 2, у 2) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:
1) точки А 1, А 2лежат по одну сторону от данной прямой, если выражения ( Ах 1+ Ву 1+ С ) и ( Ах 2+ Ву 2+ С ) имеют одинаковые знаки;
2) точки А 1, А 2лежат по разные стороны от данной прямой, если выражения ( Ах 1+ Ву 1+ С ) и ( Ах 2+ Ву 2+ С ) имеют разные знаки;
3) одна или обе точки А 1, А 2лежат на данной прямой, если одно или оба выражения соответственно ( Ах 1+ + Ву 1+ С ) и ( Ах 2+ Ву 2+ С ) принимают нулевое значение.
5. Центральный пучок– это множество прямых, проходящих через одну точку М ( х 1, у 1), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у – у 1= к ( х – х 1) ( параметр пучка к для каждой прямой свой).
Все прямые пучка можно представить уравнением: l ( y – y 1) = m ( x – x 1), где l, m – не равные одновременно нулю произвольные числа.
Если две прямые пучка L 1и L 2соответственно имеют вид ( А 1 х + В 1 у + С 1) = 0 и ( А 2 х + В 2 у + С 2) = 0, то уравнение пучка: m 1( А 1 х + В 1 у + С 1) + m 2( А 2 х + В 2 у + С 2) = 0. Если прямые L 1и L 2пересекающиеся, то пучок центральный, если прямые параллельны, то и пучок параллельный.
6. Пусть даны точка М ( х 1, у 1) и прямая, заданная уравнением Ах + Ву + С = 0 . Расстояние d отэтой точки М до прямой:
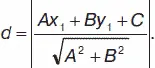
3. Полярные параметры прямой. Нормальное уравнение прямой. Преобразование координат
Полярными параметрамипрямой L будут полярное расстояние р (длина перпендикуляра, проведенного к данной прямой из начала координат) и полярный угол α (угол между осью абсцисс ОХ и перпендикуляром, опущенным из начала координат на данную прямую L ). Для прямой, представленной уравнением Ах + Ву + С = 0: полярное расстояние
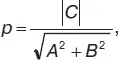
полярный угол α
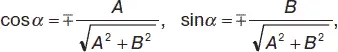
причем при C > 0 берется верхний знак, при C < 0 – нижний знак, при С = 0 знаки берутся произвольно, но либо оба плюса, либо оба минуса.
Нормальное уравнение прямой(уравнение в полярных параметрах) (cм. рис. 2): x cos α + y sin α – p = 0 . Пусть прямая представлена уравнением вида Ах + Ву + С = 0. Чтобы данное уравнение привести к нормальному виду необходимо последнее разделить на выражение 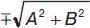 (знак берется в зависимости от знака С ).
(знак берется в зависимости от знака С ).
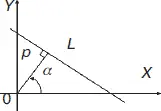
Рис. 2
После деления получается нормальное уравнение данной прямой:
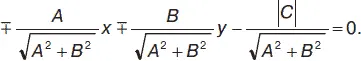
Пусть имеется прямая L , которая пересекает оси координат. Тогда данная прямая может быть представлена уравнением в отрезках х / а + у / b = 1. Справедливо: если прямая представлена уравнением х / а + у / b = 1, то она отсекает на осях отрезки а, b .
Преобразование координат возможно путем переноса начала координат, или поворотом осей координат, или совместно переносом начала и поворотом осей.
Читать дальше

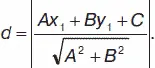
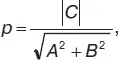
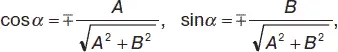
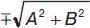 (знак берется в зависимости от знака С ).
(знак берется в зависимости от знака С ).