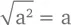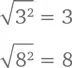Ингве Фогт - Математические трюки для быстрого счёта

Первое правило на удивление простое. Порядок чисел при умножении роли не играет:

a × b = b × a

Если буквы вам не по душе, могу продемонстрировать то же самое на простейшем цифровом примере.

3 × 7 даст тот же результат, что 7 × 3. Итак, то, в каком порядке перемножать числа, совершенно не важно.

Второе правило тоже манна небесная для тех, кто пребывает в заблуждении и считает математику сложной.

Порядок чисел при сложении роли не играет.

a + b = b + a

И вот вам пример: 2 + 3 дадут в результате то же число, что и 3 + 2.

Квадрат определенного числа выглядит следующим образом: a × a = a 2.

Обратите внимание на крошечную цифру 2 над последней «а» – читая эту книгу, вы успеете близко с ней познакомиться. Математики называют такие цифры степенями.

Вот еще пример: 3 × 3 можно обозначить как 3 2.

Разумеется, отрицательные числа тоже можно возводить в квадрат:

(‒a) × (‒a) = (‒a) 2= a 2

Например: (‒3) × (‒3) соответствует (‒3) 2.

А вот это невероятно красиво:

(‒3) 2дает тот же результат, что и 3 2.

На квадратные корни тоже приятно посмотреть:

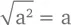
Это означает, что если извлечь квадратный корень из возведенного в квадрат числа, то это же число и получится.

На языке цифр это выглядит вот так:

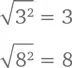
Когда надо умножать отрицательные числа, многие впадают в ступор. Если вас это тоже касается, то быстрому счету вам придется учиться долго.

Одно из важнейших правил звучит так: минус на минус дает плюс.

(‒x) × (‒y) = x × y

Примеры:

(‒2) × (‒3) = 2 × 3 = 6

(‒4) × (‒5) = 4 × 5 = 20

А вот если минус умножить на плюс, то получится, наоборот, минус:

(‒x) × y = ‒(x × y)

Примеры:

(‒2) × 3 = ‒(2 × 3) = ‒6

4 × (‒5) = ‒(4 × 5) = ‒20

Запомним это – минус на минус и минус на плюс, и тогда все минусы математики превратятся для вас в плюсы!

Если хотите понять доказательства приведенных в этой книге методов, придется научиться разлагать числовые выражения на множители и раскрывать скобки:

a(b + c) = ab + ac

(a + c)(b + d) = ab + ad + cb + cd

Вот и все – больше про разложение на множители знать нам ничего не понадобится.

Некоторые методы быстрого счета в этой книге основаны на трех видах квадратичных тождеств, которые включены в стандартную школьную программу. Все они – особые случаи правила 6:

(a + c)(b + d) = ab + ad + cb + cd

Квадратичное тождество первого типа:

(a + b) 2= a 2+ 2ab + b 2

Квадратичное тождество второго типа:

(a ‒ b) 2= a 2‒ 2ab + b 2

Квадратичное тождество третьего типа:

(a + b)(a ‒ b) = a 2‒ b 2

С этими семью правилами в готовальне у вас есть все шансы стать чемпионами быстрого счета. Ну что ж, пора отправляться завоевывать мир! Удачи и успехов!

В начальной школе я терпеть не мог спорт, зато мечтал стать чемпионом мира по решению в уме всяких математических примеров. Поэтому мне казалось ужасно несправедливым, что школьные спортсмены то и дело выступали на разных соревнованиях, ведь соревнований по математике просто не существовало. Сейчас-то я понимаю, что мое мнение о собственных математических способностях было необоснованно завышенным, я жил в мечтах: хотя считал я и правда довольно быстро, а числа так просто обожал, моих способностей не хватало, если числа в примерах были больше приведенных в таблице умножения. Впрочем, об этом никто не догадывался. Слухи о моих феноменальных математических способностях разлетались со скоростью света и с действительностью ничего общего не имели. Никогда не забуду, как мама одного из моих одноклассников на глазах у всего класса погладила меня по голове и выразила свое восхищение: еще бы, ведь я умею в уме перемножать многозначные числа. Мне тогда было девять лет. А еще мама моего одноклассника слышала, будто я умею и миллионы перемножать. Все это было неправдой, но стеснительность помешала мне опровергнуть слухи. Я смотрел на эту женщину и вспоминал, как однажды, будучи первоклашкой, возвращался из школы домой и был пойман шестиклассниками, которые потребовали сделать за них домашку по математике. Они крепко держали меня (впрочем, особых усилий от них не требовалось – я был самым мелким во всей школе) и, пока я не решил все задачки, не отпускали.