Ivan Treschev - Discrete Math. Practice. For students of technical specialties

Solution: select the forbidden pairs: (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9). To solve, we apply the main theorem of combinatorics.

To do this, define what the object is and what the properties are. By objects we mean various arrangements of camels. In total there will be N = 9!. By properties we mean the presence of a certain pair in the permutation. Thus, the number of properties is 8. Then the number of permutations that do not have any of the 8 properties:

N (8) =9! -C 8 1*8!+ C 8 2*7! -C 8 3*6! + C 8 4*5! -C 8 5*4! + C 8 6*3! -C 8 7*2! + C 8 8*1!=142729

Answer:142729.

Task number 22: preference. Cards are laid out in 3 piles and 2 cards are placed in the draw. Play 32 cards, i.e. each player receives 10 cards. Determine the number of layout options.

Solution: using the formula of permutations with repetitions we get: ((32!) \ (10! 3*2!))

Answer: ((32!) \ (10! 3*2!)).

Task number 23: from a group of 15 people it is necessary to select a team, which should include at least 5 people. How many choices.

Solution: we calculate the number of unfavorable combinations of choice, i.e., we compose options for brigades of 1, 2, 3, 4 people. Their number is: C 15 1+ C n15 2+C 15 3+ C 15 4=1940.

And the total number of brigades is 2 15. The difference gives the number of noble combinations.

Answer: 2 15 – 1914.

Task number 24: three boys picked 10 apples. How many ways are there to split apples between them.

Solution: We write 10 units and 2 zeros that perform the functions of a separator, and then we begin to rearrange them with all possiblemethods. Each permutation will correspond to some way of dividing 10 apples into 3 heaps. Each section method will correspond to some code containing 10 units and 2 zeros. Therefore, the number of partition methods: P (10.2) = ((10!) \ (2!8!)) =45

Answer: 45.

Problem number 25: a set of 8 elements is necessary to find the number of its partitions.

Solution: The number of partitions of the set is the Bell number => B 8=4140.

Answer: 4140.

Problem number 26: find the number of decimal non-negative integers, consisting of numbers, arranged in increasing order.

Solution: 1+ C 9 1+…C 9 9=2 10.

Answer: 2 10

Problem number 27: how many word decompositions from the letters ABRAKADABRA

Solution: in the word ABRAKADABRA there are 11 letters, of which five are letters A, two letters B and two letters R. So, we get by the formula of permutations with repetitions, we get: P n = ((11!) \ (5!*2! *2!)) =83160

Answer: 83160.

Problem number 28: find the sum of all divisors of 300.

Solution: 300 = 1+2+3+4+5+6+10+12+15+20+25+30+50+60+75 +100+150 +300 = 868

Answer: 868. This problem can be solved using the Euler formula.

Problem number 29: How many numbers between 1000 and 10000 consist of:

– odd numbers;

– different numbers.

Solution:

a) Between 1000 and 10000 are four-digit numbers. Because numbers consist only of odd numbers, then the first digit can be selected in 5 ways (digits 1, 3, 5, 7 and 9), the second, third and fourth digit can also be selected in 5 ways (digits 1, 3, 5, 7 and 9). Therefore, there will be a total of such numbers: n=5*5 *5 *5=625

b) numbers consist of various digits, then the first digit can be selected in 9 ways (digits 1, 2, 3, 4, 5, 6, 7, 8 and 9), the second digit in 9 ways (there can be 0 and any of the previous ones, but not repeating), the third digit in 8 ways and the fourth digit in 7 ways. Therefore, there will be a total of such numbers: n=9*9 *8 *7=4536

Answer: a) 625; b) 4536.

The task №30: prove | √ |x||=√x||.

Solution: Let m = | √ |x||

Because the rules ≤ |x|=n <=> nx

m 2 ≤ |x| ( 2

From the rules: x <=> |x|

n ≤x <=> n <|x|,where nan integer

must be m 2 ≤ x ( 2

m ≤ √ x

From (*) => m= | √

Thus | √ |x||= m= | √x|.

Problem No. 31: u n +2 = -u n +1 +2u n,u 0 = 0, u 1 = 1

Solution: here K (x) =1+x-2x 2. We calculate: D (x) =K (x) u (x) = (1+x-2x 2) (u 0 + u 1x+…) 0+x+0=x

We get: u (x) = ((x) \ (1+x-2x 2))

The next step is the expansion of the denominator K (x) to the product (a 1—1x) (1a 2x), then 〈 1 and 〈 2 – the roots of the quadratic equation: 1+x-2x 2=0

and

a 1=1

a 1= ((-1) \ (2))

arrive to the formula: u (x) = ((x) \ (12+x-x 2)) = ((x) \ ((1-x) (1+ ((x) \ (2)))))

We find the decomposition into a sum of simple fractions by the method of indefinite coefficients: ((x) \ ((1-x) (1+ ((x) \ (2))))) = ((A) \ ((1-x))) + ((B) \ (1+ ((x) \ (2))))

We obtain a system of linear equations: ((1) \ (2)) AB=1B+A=0

Its solution: A= ((2) \ (3)),B= ((-2) \ (3)). Hence: u (x) = (((2) \ (3)) \ (1-x)) + (((-2) \ (3)) \ (1- ((x) \ (2)))) = ((2) \ (3)) ∑ k=0 ∞1 kx k– ((2) \ (3)) ∑ k=0 ∞ ((-1) \ (3)) kx k

This leads to the answer: u n= ((2) \ (3)) – ((2) \ (3)) * ((-1) \ (2)) n

Answer: u n= ((2) \ (3)) – ((2) \ (3)) * ((-1) \ (2)) n

Task number 32: 15 students shook hands at a meeting of students, three people made 4 handshakes, and others – 3. How many students were there.

Solution: We will consider a case requiring a smaller number of participants. Since the three made 4 handshakes: we consider. That between them they made maximum handshakes – two, and formed a complete 3x vertex graph and used only 3 handshakes out of the total:

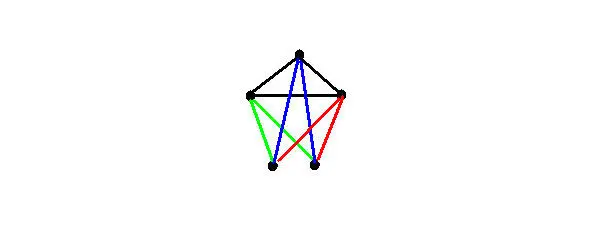
Each «had» two handshakes. The minimum number of vertices that must be added so that the condition «three made 4 handshakes» is met – these are two. Let’s portray them like this:

We get already 9 used handshakes. And the two added vertices have 3 handshakes, which corresponds to the condition. It remains 6. Just the full 4-vertex graph gives us 6 handshakes for each of the 4 students added:

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.