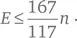Иэн Стюарт - Математические головоломки профессора Стюарта

– Могу я их переворачивать?

– Прекрасный вопрос! Да, любую плитку можно перевернуть.

Я немного поэкспериментировал. Внезапно ответ встал перед глазами.

– Сомс! Из них получается квадрат – узор Беатрис! Как красиво!

Сомс взглянул на мою небольшую головоломку.

– В самом деле. Вы по-прежнему утверждаете, что элегантное объяснение нескольких улик может служить определяющим доказательством того, что виновный найден?

– Как иначе все улики могут так сойтись, Сомс?

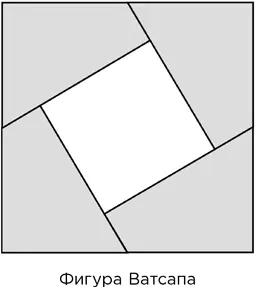
– В самом деле, как? – я понял, что вопрос был риторическим. – В ваших рассуждениях есть прореха, Ватсап, – продолжал он, когда я отказался отвечать. – Нужно ее устранить, – он наклонился и переложил плитки так, что получился заполненный квадрат.

– Ох, – пристыженно произнес я. – Значит, это – узор Беатрис.

– Предполагаю, что да. Но не расстраивайтесь: ваш узор принадлежит мисс Мейкпис.

Меня осенило.

– Вы думаете, что из копий одной этой плитки можно сложить все 13 узоров?

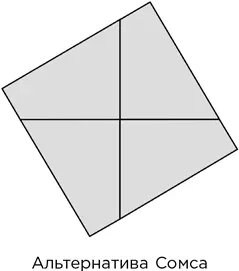
– Я в этом уверен. Смотрите: вот так из трех плиток складывается узор миссис Уоттон, равносторонний треугольник с треугольным отверстием.

– Господи, Сомс!

– Это замечательно универсальная… э-э… плитка, – ответил он. – Благодарить за это нужно ее хитрую геометрию.

– Итак, все, что нам нужно сделать… – начал я.

– …это найти варианты раскладки, соответствующие остальным десяти узорам! – закончил за меня Роулейд.

Сомс начал прочищать трубку.

– Я уверен, что смело могу оставить эту задачу вам, джентльмены.

В тот вечер я взял кэб и поехал в дом отца Беатрис, остановившись только у ювелира, чтобы кое-что забрать. Беатрис приняла меня в гостиной.

Я поставил на стол длинную коробочку.

– Дорогая, откройте.

Она несмело протянула руку, и на милом лице ее отразилась надежда.

– О! Джон, вы нашли мою подвеску! – она взяла меня за руку. – Как я могу отблагодарить вас? – внезапно она замолчала. – Но… Это не мое, – она вынула из коробки сверкающую драгоценность. – Это обручальное кольцо.

– Да, это так. И оно может стать вашим, – произнес я, опускаясь на одно колено.

Можете ли вы найти оставшиеся десять вариантов узора? Ответы см. в главе «Загадки разгаданные».

Граф – это набор точек (узлов), соединенных линиями (ребрами). Если граф рисуют на плоскости, ребра часто пересекаются между собой. В 1972 г. Джон Конвей определил трекл как граф, нарисованный на плоскости, у которого любые два ребра либо встречаются в узле и больше не пересекаются, либо не встречаются в узле, но при этом пересекаются ровно один раз. Говорят, что идею названия подал автору один шотландский рыболов, постоянно жаловавшийся на то, что у него запуталась (thrackled) леска.

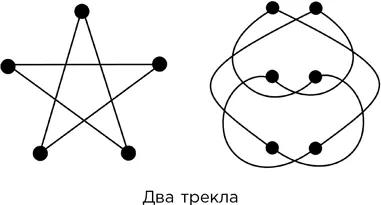
На рисунке показаны два трекла. Левый имеет в своем составе 5 узлов и 5 ребер, тогда как правый – 6 узлов и 6 ребер. Конвей предположил, что у любого трекла число ребер меньше или равно числу узлов. Он предложил бутылку пива в награду тому, кто сможет это доказать или опровергнуть, но с годами, поскольку решение не появлялось, приз вырос до тысячи долларов.

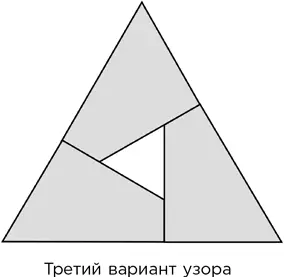
Оба приведенных трекла представляют собой замкнутые петли (их узлы располагаются на кольцевом маршруте), нарисованные с наложением. Известно, что любая замкнутая петля с n ³ 5 узлов может быть нарисована так, что образует трекл. Если это правда, то число E ребер может быть равно числу n узлов при любом n ³ 5. Пал Эрдёш доказал, что гипотеза о трекле верна для любого графа с прямыми ребрами. Наилучшее на данный момент ограничение на размер E доказали Радослав Фулек и Янош Пач в 2011 г.:

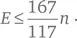
Ссылку на дополнительную информацию см. в главе «Загадки разгаданные».

Один математик, потративший десять бесплодных лет на попытки доказать гипотезу Римана, решил продать душу дьяволу в обмен на вожделенное доказательство. Дьявол обещал представить ему доказательство не позже чем через неделю, но неделя прошла, и ничего не произошло.