Иэн Стюарт - Математические головоломки профессора Стюарта

Действительно, математики, которые первыми выдвинули эти идеи, не думали ни о каких конкретных практических приложениях для них; просто квадратичные вычеты показались им интересными. Но они также были убеждены, что их понимание станет новым мощным дополнением к математическому инструментарию. Практики не в состоянии пользоваться инструментом, пока его не существует. И хотя на первый взгляд может показаться, что разумнее подождать появления конкретной задачи, прежде чем придумывать инструменты, подходящие для ее решения, при таком подходе мы до сих пор жили бы в пещерах. «Зачем ты теряешь время, стуча камнем по камню, а, Уг? Тебе следовало бы стучать палкой по голове мамонта, как делают остальные мальчики».

У квадратичных вычетов множество самых разных применений. Один из моих любимых примеров – проектирование концертных залов. Музыка, отражаясь от плоского потолка, дает явственное эхо, которое искажает звук и вообще мешает слушать. С другой стороны, звукопоглощающий потолок делает звучание мертвым и смазанным. Для хорошей акустики звук должен отражаться, но в виде рассеянного отзвука, а не резкого эха. Поэтому архитекторы встраивают в потолок специальные рассеиватели. Вопрос в том, какой они должны быть формы.

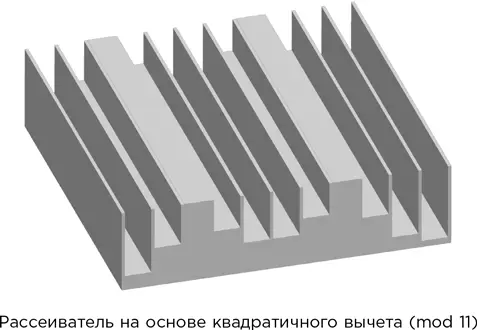
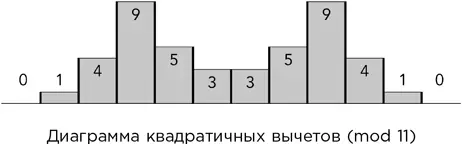
В 1975 г. Манфред Шрёдер изобрел рассеиватель, состоящий из серии параллельных борозд, глубина которых выводится из последовательности квадратичных вычетов для некоего простого модуля. Возьмем, к примеру, простое число 11. Мы только что видели, что квадраты чисел от 0 до 10 по модулю 11 равны:

0 1 4 9 5 3 3 5 9 4 1,

и далее, для более крупных чисел, эта последовательность повторяется периодически. Она симметрична относительно середины, промежутка между двумя тройками, потому что x ² = (– x )² по любому простому модулю. Сравним рисунок ниже – на нем эти числа показаны в виде прямоугольников – с формой рассеивателя на предыдущем рисунке. Обратите внимание: в данном случае глубина выемок получается путем вычитания вычетов из какой-то постоянной величины. Это не оказывает серьезного влияния на основной математический смысл.

Что такого особого в квадратичных вычетах? Одна из характеристик звуковой волны – ее частота: сколько волн приходит в ухо каждую секунду. Высокие частоты дают высокие звуки, низкие частоты – низкие звуки. Еще одна характеристика, связанная с частотой, – длина волны: расстояние между последовательными пиками. Высокочастотные волны короче, низкочастотные – длиннее. Колебания с заданной длиной волны резонируют с пустотами в поверхности, размеры которых близки к длине их волны. Так что волны разных частот по-разному реагируют на столкновение с поверхностью.

Рассеиватель на основе квадратичных вычетов обладает восхитительным математическим свойством: волны различных частот взаимодействуют с ним одинаково. Технически это означает, что преобразование Фурье постоянно на некотором диапазоне частот. Шрёдер указал на одно важное следствие: такая форма рассеивает звуковые волны многих разных частот одинаково. На практике ширина бороздок выбирается так, чтобы избежать диапазона волн, доступных для человеческого уха, а их длина кратна с определенным коэффициентом последовательности квадратичных вычетов, связанных с шириной.

Когда бороздки параллельны, как на рисунке, звук рассеивается в стороны, под прямым углом к бороздкам. Существует двумерный аналог этой системы – квадратное поле со стержнями, тоже рассчитанными на основе квадратичных вычетов, – который рассеивает звук равномерно во всех направлениях. Такие рассеиватели часто можно найти в звукозаписывающих студиях, где они помогают улучшить звуковой баланс и избавиться от лишних шумов.

Так что хотя Эйлер и Гаусс понятия не имели, для чего когда-нибудь будет использовано их изобретение и будет ли оно использовано хоть для чего-то, оно нередко играет принципиально важную роль (неявно, где-то за сценой), когда вы слушаете записанную музыку, будь то классика, джаз, кантри, рок, хип-хоп, кроссовер-трэш металлика – все что угодно.

Дополнительную информацию см. в главе «Загадки разгаданные».