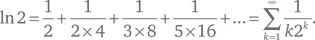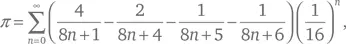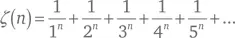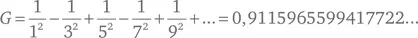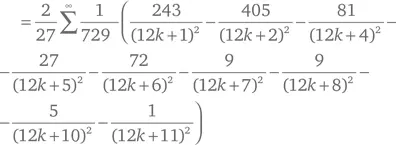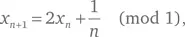Иэн Стюарт - Математические головоломки профессора Стюарта

В 2011 г. Дэвид Бейли, Джонатан Боруэйн, Эндрю Маттинли и Гленн Уайтвик составили обзорное исследование этого вопроса [27] David Bailey, Jonathan Borwein, Andrew Mattingly, and Glenn Wightwick. The computation of previously inaccessible digits of π2 and Catalan's constant, Notices of the American Mathematical Society 60 (2013) 844–854. . Авторы описали способ нахождения знаков числа π² в системе счисления с основанием 64, знаков числа π² в системе счисления с основанием 729 и знаков числа, известного как постоянная Каталана, в системе счисления с основанием 4096, начиная с 10-триллионной позиции.

История начинается с последовательности, известной еще Эйлеру:

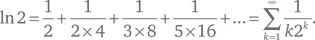
Благодаря степеням двойки, которые здесь фигурируют, этот ряд можно преобразовать в метод вычисления конкретных двоичных знаков ln 2. По мере роста номера знака вычисления остаются реализуемыми, хотя и занимают гораздо больше времени.

Формула ББП выглядит так:

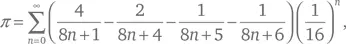
и степени 16 делают возможным вычисление конкретных шестнадцатеричных знаков числа π. Поскольку 16 = 2 4, ряд можно использовать также для вычисления двоичных знаков.

Ограничивается ли такой подход только этими двумя константами? С 1997 г. математики ведут непрекращающийся поиск аналогичных бесконечных рядов для других постоянных величин, и им уже удалось найти их немалое количество. В том числе для π², ln² 2, π ln 2, ζ (3), π³, ln³ 2, π²ln 2, π 4, ζ (5),

где

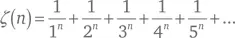
есть Риманова дзета-функция. Удалось сделать то же для постоянной Каталана

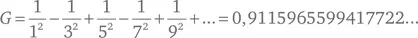
Некоторые из этих рядов дают знаки в троичной системе счисления или системе с основанием, равным какой-нибудь степени 3. К примеру, при помощи поразительной формулы Дэвида Броудхерста

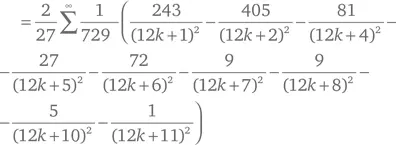
можно вычислять знаки π² в системе счисления с основанием 729 = 3 6.

Десятичные знаки числа π кажутся случайными, но они не могут быть по-настоящему случайными, потому что всякий раз при вычислении числа π вы получаете ровно одно и то же (если, конечно, не ошибаетесь в процессе вычисления). Считается, что, как почти в любой случайной последовательности цифр, где-то в десятичном выражении числа π встречается любая конечная последовательность цифр. Более того, данная последовательность встречается бесконечно часто, хотя и с кучей мусора между двумя последовательными включениями, и в той же пропорции, которую следовало бы ожидать для случайной последовательности.

Можно доказать, что это свойство, известное как нормальность, выполняется для «почти всех» чисел: в любом достаточно большом наборе чисел доля нормальных подходит сколь угодно близко к 100 %. Но это правило оставляет и лазейку, поскольку любое конкретное число, скажем π, может оказаться исключением. Но является ли оно исключением? Мы не знаем. До недавнего времени этот вопрос казался безнадежным, но формулы, подобные приведенным выше, открыли новую линию атаки, которая в принципе может решить вопрос в отношении двоичных (или шестнадцатеричных) чисел.

Связь между этими задачами возникает через другую математическую процедуру, итерационную. Здесь мы начинаем с какого-то числа, применяем к нему некое правило, чтобы получить другое число, и последовательно применяем то же правило к полученным числам, чтобы получить некую последовательность чисел. К примеру, если мы начнем с 2 и применим правило «возвести в квадрат», получим последовательность

2 4 16 256 65 636 4 294 967 296 …

Двоичные знаки числа, к примеру ln 2, можно получить при помощи итерационной формулы

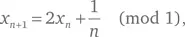
начиная с x 0 = 0. Пояснение (mod 1) означает «вычесть целую часть», так что π (mod 1) = 0,14159… Эта формула привела бы к доказательству того, что ln 2 нормален по основанию 2, если бы удалось показать, что полученные в результате числа равномерно распределены по интервалу от 0 до 1. Подобная «равнораспределенность» встречается довольно часто. К несчастью, никто не знает, как доказать, что она распространяется на приведенную итеративную формулу, но сама по себе эта идея перспективна и, вполне возможно, со временем даст результат.