Иэн Стюарт - Математические головоломки профессора Стюарта

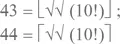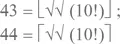
требуют только двух единиц, так что мы немедленно заполняем все пропуски между 26 и 61. Возникает пробел на 62 (потому что это 44 + 18, а на выражении 18 через две единицы мы застряли), но 63 и 64 у нас есть. Далее, опираясь на 80, мы можем добраться до 97. На 98 опять возникает пробел, но 99 и 100 можно получить.

– И намного проще, кстати говоря, – заметил Сомс:

99 = 11/0,1 × 0,1;

100 = 1/(0,1 × 0,1);

101 = 1/(0,1 × 0,1) + 1.

– Таким образом, у нас есть все вплоть до 100, – сказал я, – за исключением 62 и 98.

– Но о 98 позаботится 105, вместе со всеми остальными числами вплоть до 122, – сказал Сомс.

– О, я и забыл, что у нас есть 105 из двух единиц.

– А поскольку 120 = 5! то есть тоже выражается через две единицы, мы можем добраться до 137. Более того, у нас есть еще 139 и 140.

– Так что единственные пробелы до 140 – это 62 и 138, – сказал я.

– Похоже на то, – сказал Сомс. – Интересно, можно ли заполнить эти пробелы каким-то другим способом?

Сможете ли вы найти способ записать 62 и 138 при помощи четырех единиц, не используя ничего более эзотерического, чем те функции, которые Сомс и Ватсап уже использовали? Ответ см. в главе «Загадки разгаданные».

Сомс и Ватсап все еще не закончили. Но финал уже близок: «Знак одного» завершается в главе «Знак одного. Часть четвертая – завершение».

Сриниваса Рамануджан – индийский математик-самоучка с поразительным талантом к формулам, как правило очень странным формулам, обладавшим, однако, своеобразной необычной красотой. В 1914 г. математики Годфри Харолд Харди и Джон Эденсор Литтлвуд из Кембриджа привезли его в Англию. К 1919 г. у него уже были неизлечимо больные легкие, и в 1920 г. он умер в Индии. Харди писал:

«Помню, как я однажды поехал навестить его, когда он лежал больной в Путни. Я приехал в такси номер 1729 и заметил вскользь, что номер этот показался мне довольно скучным и что я надеюсь, что это не дурное предзнаменование. „Нет, – ответил он, – это очень интересный номер; это наименьшее число, которое можно выразить в виде суммы двух [положительных] кубов двумя разными способами“».

Наблюдение о том, что

1729 = 1³ + 12³ = 9³ + 10³,

впервые опубликовал Бернар Френикль де Бесси в 1657 г. Если разрешить отрицательные кубы, то наименьшим таким числом будет

91 = 6³ + (–5)³ = 4³ + 3³.

Специалисты по теории чисел обобщили эту концепцию, заявив, что n -й номер такси Ta ( n ) есть наименьшее число, которое можно выразить в виде суммы двух положительных кубов n и другими способами.

В 1979 г. Харди и Э. М. Райт доказали, что некоторые числа могут быть выражены в виде суммы произвольно большого числа положительных кубов, так что Ta ( n ) существует для любых n . Однако вплоть до настоящего времени известны лишь первые шесть таких чисел:

Ta (1) = 2 = 1³ + 13;

Ta (2) = 1729 = 1³ + 12³ = 9³ + 10³;

Ta (3) = 87539319 = 167³ + 436³ = 228³ + 423³ = 255³ + 414³;

Ta (4) = 6963472309248 = 2421³ + 19083³ = 54363 + 18948³ = 10200³ + 18072³ = 13322³ + 166308³;

Ta (5) = 48988659276962496 = 38787³ + 3657573 = 107839³ + 362753³ = 205292³ + 342952³ = 221424³ + 336588³ = 231518³ + 331954³;

Ta (6) = 24153319581254312065344 = 582162³ + 28906206³ = 3064173³ + 28894803³ = 8519281³ + 28657487³ = 16218068³ + 27093208³ = 17492496³ + 26590452³ = 18289922³ + 26224366³.

Ta (3) открыл Джон Лич в 1957 г. Ta (4) нашли Э. Розенстил, Дж. А. Дардис и К. Р. Розенстил в 1991 г. Ta (5) обнаружил Дж. А. Дардис в 1994 г. и подтвердил Дэвид Уилсон в 1999 г. В 2003 г. К. С. Калуд, Э. Калуд и М. Дж. Диннин установили, что приведенное выше число, вероятно, является Ta (6), а в 2008 г. Уве Холлербах опубликовал доказательство.

Математические исследования верхом?

Почему бы нет? Вдохновение может осенить где угодно. Выбирать не приходится.

В 1834 г. шотландский инженер-кораблестроитель Джон Скотт Рассел, ехавший на лошади вдоль канала, обратил внимание на поразительное явление:

«Я наблюдал за движением лодки, которую стремительно тянула по узкому каналу пара лошадей, как вдруг лодка остановилась – лодка, но не та масса воды в канале, которую она увлекла и приводила в движение; эта вода собралась вокруг носа судна в состоянии неистового возбуждения, затем внезапно оторвалась от него и покатилась вперед с огромной скоростью, принимая форму большого одиночного возвышения, округлой, гладкой и четко очерченной водяной массы, которая продолжила движение вдоль канала без всякого видимого изменения формы или снижения скорости. Я последовал за ней верхом и догнал; она катилась дальше со скоростью примерно 13 или 15 км/ч, сохраняя первоначальную форму, размером около 9 м в длину и 30–45 см в высоту. Ее высота постепенно снижалась, и после преследования на протяжении 1,5–3 км я потерял ее среди извивов канала. Вот такой в августе 1834 г. была моя первая случайная встреча с этим исключительным и красивым явлением, которое я назвал волной перемещения».