Иэн Стюарт - Величайшие математические задачи

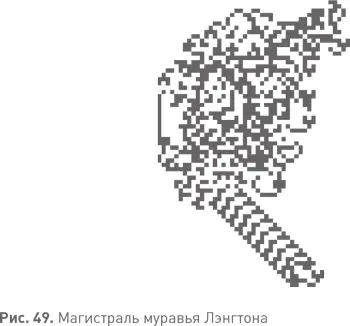
Все описанное до сих пор может быть доказано по всей строгости просто последовательным перебором муравьиных шагов. Это будет достаточно длинное доказательство — список из 10 000 шагов, — но все же доказательство. Но математика системы станет более интересной, если мы зададимся чуть более общим вопросом. Что если еще до начала движения муравья мы перекрасим некоторое конечное число клеток решетки в черный цвет? Мы можем выбрать для этого любые клетки: это может быть случайный набор, черный квадрат или Мона Лиза. Их может быть миллион, или миллиард, или еще больше, но не бесконечное количество. Что произойдет?

Обычное движение муравья резко меняется при встрече с любой из новых черных клеток. Он может долго бродить окрест, рисуя сложные орнаменты и раз за разом перерисовывая их заново… Но во всех до сих пор предпринятых попытках, какой бы ни была первоначальная конфигурация, в конце концов муравей непременно принимался за строительство магистрали при помощи все того же 104-шагового цикла. Всегда ли это происходит? Является ли магистраль единственным «аттрактором» движения муравья? Никто не знает. Это одна из фундаментальных нерешенных задач теории сложности. Максимум, что нам известно, — это то, что, какой бы ни была первоначальная конфигурация черных клеток, муравей не останется навечно в пределах ограниченной области поля.

Матрица Адамара, названная в честь Жака Адамара, представляет собой квадратную матрицу из нулей и единиц, такую, что в любых двух ее рядах или столбцах половина элементов совпадает, а другая половина — отличается. На рис. 50 можно увидеть матрицы размеров 2, 4, 8, 12, 16, 20, 24 и 28, где 0 и 1 обозначены черным и белым цветом. Такие матрицы появляются во многих математических задачах и в компьютерных науках, в первую очередь в теории кодирования. (В некоторых приложениях, в том числе в задаче, которой первоначально занимался Адамар, белые квадраты соответствуют −1, а не 0.)

Адамар доказал, что подобные матрицы могут существовать только при n = 2 или n, кратном 4. Теорема Пейли 1933 г. доказывает, что матрица Адамара существует всегда для n , кратного 4 и равного 2 a ( p b + 1), где p — нечетное простое число. Из чисел, кратных 4, под эту теорему не подпадают 92, 116, 156, 172, 184, 188, 232, 236, 260, 268 и другие, более крупные значения n . Гипотеза утверждает, что матрица Адамара существует любых размеров, кратных 4. В 1985 г. К. Савад нашел матрицу размера 268. Есть и другие числа, не удовлетворяющие условию теоремы Пейли, с которыми уже разобрались. В 2004 г. Хади Харагани и Бехруз Тайфех-Резайе нашли матрицу Адамара размера 428, и теперь минимальное значение n, для которого она неизвестна, составляет 668.

Это диофантово уравнение x a+y b= z c , где a, b и c — положительные целые числа, показатели степени. Я назову это уравнение уравнением Ферма — Каталана, потому что его решения имеют отношение как к Великой теореме Ферма (см. главу 7), так и к гипотезе Каталана (см. главу 6). Если a, b и c малы, ненулевые целые решения не особенно удивительны. К примеру, если все они равны 2, мы имеем уравнение Пифагора, которое, как известно со времен Евклида, имеет бесконечно много решений. Так что основной интерес представляют те случаи, когда показатели степени велики. Формально они являются «большими», когда s = 1/ a + 1/ b + 1/ c меньше 1. Известно лишь десять больших решений уравнения Ферма — Каталана:

1 + 2³ = 3²,

2 5+ 7 2= 3 4,

7 3+ 13 2= 2 9,

2 7+ 17 3= 71 2,

3 5+ 11 4= 122 2,

17 7+ 76 271 3= 21063928 2,

1414 3+ 2213459 2= 65 7,

9262 3+ 15312283 2= 113 7,

43 8+ 9622 3= 30042907 2,

33 8+ 159034 2= 15613 3.

Первое из этих решений считается большим, потому что 1 = 1 a для любого a и для a = 7 в том числе. Гипотеза Ферма — Каталана утверждает, что для больших s уравнение Ферма — Каталана имеет лишь конечное число целых взаимно простых решений. Основной результат доказали в 1997 г. Анри Дармон и Лоик Мерель: не существует решений, в которых c = 3, а a и b равны и больше 3. Больше почти ничего не известно. Дальнейший прогресс, судя по всему, зависит от поразительной новой гипотезы, речь о которой пойдет ниже.