Джордан Элленберг - Как не ошибаться. Сила математического мышления

Эта борьба нигде не проявляется более отчетливо, чем в планиметрии [59]. Здесь находится последний бастион обучения построению доказательств, которые лежат в основе преподавания математики. Многие профессиональные математики считают доказательство последним оплотом «истинной математики». Однако не совсем понятно, в какой степени мы на самом деле учим красоте, силе и неожиданности доказательства в процессе преподавания геометрии. Учебный курс легко может превратиться в рутинную отработку таких бесполезных и неинтересных задач, как вычисление тридцати определенных интегралов. Это настолько серьезная ситуация, что лауреат Филдсовской премии Дэвид Мамфорд предположил: мы можем полностью отказаться от планиметрии, заменив ее начальным курсом программирования. Компьютерная программа имеет много общего с геометрическим доказательством: и то и другое требует, чтобы студент собрал один за другим воедино ряд простых элементов, выбранных из небольшой совокупности вариантов, так, чтобы в целом сформированная последовательность выполняла ту или иную значимую задачу.

Я не настолько радикален. Я вообще не отношусь к числу радикалов. Хотя это и может вызвать недовольство сторонников обоих подходов, я считаю, что мы должны преподавать математику, в которой высоко ценятся как точные ответы, так и интеллектуальная аппроксимация; математику, требующую как способности свободно применять существующие алгоритмы, так и простого здравого смысла, помогающего находить спонтанные решения; математику, в которой научная строгость сочетается с ощущением игры. Откровенно говоря, если всего этого нет, мы вообще преподаем не математику.

Трудная задача, но именно этим занимаются лучшие преподаватели математики, пока наверху среди администраторов бушуют математические войны.

Так сколько американцев будут страдать ожирением к 2048 году? Вы уже догадываетесь, как Юфа Ванг и другие авторы статьи, опубликованной в журнале Obesity, построили свою проекцию. Национальная программа проверки здоровья и питания населения (National Health and Nutrition Examination Study, далее везде – NHANES) отслеживает данные о состоянии здоровья большой репрезентативной выборки граждан, охватывающие самые разные аспекты: от потери слуха до передачи инфекций половым путем. В частности, NHANES предоставляет весьма достоверные данные о доле американцев, имеющих избыточный вес; его в данном случае можно определить как вес, при котором индекс массы тела (далее везде – ИМТ) [60]равен 25 и более [61]. Нет никаких сомнений в том, что за последние десятилетия распространенность избыточного веса увеличилась. В начале 1970-х годов чуть менее половины американцев имели столь высокий ИМТ. В начале 1990-х этот показатель возрос до 60 %, а в 2008 году избыточный вес был почти у трех четвертей населения США.

Вы можете самостоятельно построить график роста распространенности ожирения во времени, как мы сделали это с вертикальным перемещением ракеты.

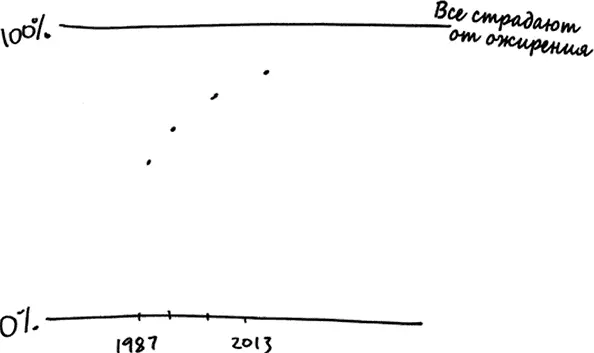
Далее вы можете сформировать линейную регрессию, которая будет выглядеть примерно так.

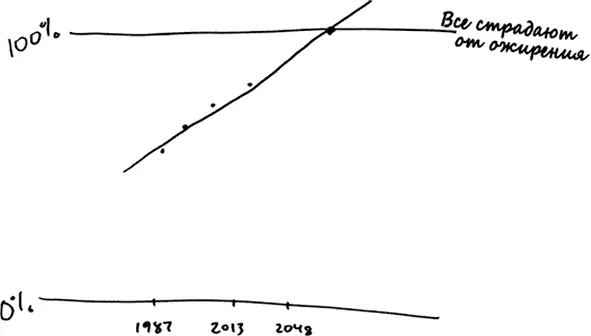
Прямая линия пересечет уровень 100 % в 2048 году. Именно поэтому Ванг пишет, что к 2048 году все американцы будут страдать избыточным весом, если текущая тенденция сохранится.

Но текущая тенденция не сохранится. Это просто невозможно! Если было бы так, то к 2060 году уже 109 % американцев имели бы избыточный вес [62].

В действительности график, отображающий рост доли людей с избыточным весом, изгибается к 100 % следующим образом.

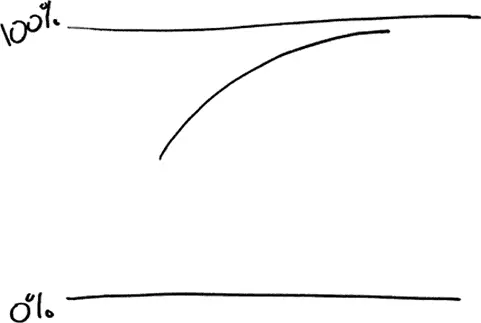
Этот закон отнюдь не незыблем, как и в случае, когда сила тяжести изгибает траекторию движения ракеты в виде параболы, однако он близок к реальности с медицинской точки зрения. Чем больше доля людей с избыточным весом, тем меньше остается худощавых людей, которые могли бы стать толстыми, и тем медленнее доля людей с избыточным весом приближается к 100 %. На самом деле в какой-то точке ниже 100 % эта кривая перейдет в горизонтальную линию. Худые всегда будут с нами! В действительности четыре года спустя по результатам опроса NHANES было установлено, что распространенность избыточного веса начала замедляться {32}.