Джордан Элленберг - Как не ошибаться. Сила математического мышления

Вы могли бы нанести на график положение ракеты по вертикали в пяти точках по времени. Такой график выглядит следующим образом.

Теперь вы в состоянии быстро выполнить линейную регрессию, получив замечательный результат: линию, которая проходит почти через все точки на графике.

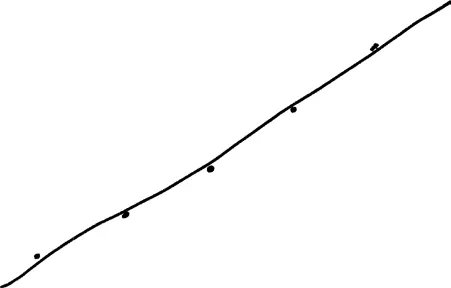
(В этот момент ваша рука начинает приближаться к острому полотнищу циркулярной пилы.)

Построенная вами линия представляет собой весьма точную модель движения ракеты: за каждую минуту ракета поднимается вверх на определенное фиксированное расстояние, скажем на 400 метров. Через час ракета окажется в 24 километрах над поверхностью земли. Когда же она опустится на поверхность? Никогда! Направленная вверх наклонная прямая линия по-прежнему стремится вверх. Именно так ведут себя прямые.

(Кровь, травмы, вопли.)

Однако не каждая линия является прямой. А траектория полета ракеты несомненно представляет собой не прямую, а параболу. Подобно окружности Архимеда, вблизи она действительно похожа на прямую, поэтому линейная регрессия сослужит вам большую службу, позволив определить местоположение ракеты через пять секунд после запуска. Но через час? Даже не думайте об этом. Ваша модель говорит о том, что через час ракета находится в нижних слоях стратосферы, хотя на самом деле она, возможно, уже приближается к вашему дому.

Возможно, самое образное предостережение в отношении бездумной линейной экстраполяции сформулировал не статистик, а Марк Твен в романе Life on the Mississippi («Жизнь на Миссисипи»):

…Длина Миссисипи между Каиром и Новым Орлеаном сто семьдесят шесть лет тому назад была тысяча двести пятнадцать миль. После прорыва русла в 1722 году длина стала тысяча сто восемьдесят миль. Когда образовался рукав у Американской излучины, длина стала тысяча сорок миль. С тех пор этот участок реки укоротился еще на шестьдесят семь миль. Следовательно, сейчас ее длина между Каиром и Новым Орлеаном всего девятьсот семьдесят три мили.

…За сто семьдесят шесть лет Нижняя Миссисипи укоротилась на двести сорок две мили, то есть в среднем примерно на милю и одну треть в год. Отсюда всякий спокойно рассуждающий человек, если только он не слепой и не совсем идиот, сможет усмотреть, что в древнюю силурийскую эпоху, – а ей в ноябре будущего года минет ровно миллион лет – Нижняя Миссисипи имела свыше миллиона трехсот тысяч миль в длину и висела над Мексиканским заливом наподобие удочки. Исходя из тех же данных, каждый легко поймет, что через семьсот сорок два года Нижняя Миссисипи будет иметь только одну и три четверти мили в длину, а улицы Каира и Нового Орлеана сольются, и будут эти два города жить да поживать, управляемые одним мэром и выбирая общий городской совет. Все-таки в науке есть что-то захватывающее. Вложишь какое-то пустяковое количество фактов, а берешь колоссальный дивиденд в виде умозаключений. Да еще с процентами [56].

Методы математического анализа во многом похожи на линейную регрессию: они носят сугубо механический характер, с ними вполне может справиться ваш калькулятор, а невнимательное применение этих методов сопряжено с большими опасностями. На экзамене по матану вам могут предложить рассчитать вес воды, оставшейся в кувшине после того, как вы проделаете в нем отверстие и позволите воде вытекать определенным потоком на протяжении определенного промежутка времени, и тому подобное. Решая задачу такого рода в условиях нехватки времени, вполне можно сделать арифметические ошибки. Порой это приводит к тому, что тот или иной студент получает нелепый результат, например что вес воды в кувшине составляет −4 грамма.

Если студент получает результат «−4 грамма» и в отчаянии торопливо пишет «Я где-то напортачил, но не могу найти ошибку», я даю такому студенту половину зачетных баллов за экзамен.

Если же студент просто пишет «−4 грамма» в конце страницы и обводит этот результат кружком, он получает ноль зачетных баллов – даже если вся процедура вывода этого результата была правильной, за исключением того, что где-то посередине страницы единственная цифра оказалась не на своем месте.