Джордан Элленберг - Как не ошибаться. Сила математического мышления

ожидаемое количество пересечений иглы длиной N = Np

верна для любого положительного действительного числа N , будь то большого или малого.

(Здесь не стоит приводить строгое доказательство того, что представленная выше формула применима и в случае, когда N – некое страшное иррациональное число, скажем квадратный корень из 2, потому что для этого понадобятся формальные математические выкладки. Но я даю честное слово, что основные идеи доказательства Барбье – те, что я привел.)

Теперь необходимо проанализировать задачу под новым, так сказать, углом, согнув иглу.

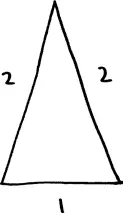
Это самая длинная игла из всех, с которыми мы до сих пор имели дело: ее общая длина равна 5 единицам. Однако эта игла согнута в двух местах, а два ее края я сомкнул, чтобы образовать треугольник. Прямые сегменты иглы имеют длину 1 единица, 2 единицы и 2 единицы; следовательно, ожидаемое количество пересечений каждого сегмента равно p , 2 p и 2 p соответственно. Количество пересечений всей иглы равно сумме количества пересечений каждого сегмента. Таким образом, принцип аддитивности говорит нам, что ожидаемое количество пересечений целой иглы составляет:

p + 2 p + 2 p = 5 p .

Другими словами, формула

ожидаемое количество пересечений иглы длиной N = Np

применима и в случае согнутых игл.

Вот одна из таких игл.

Вот еще одна.

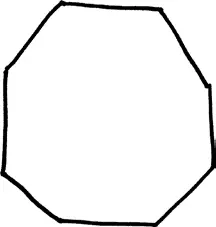
И еще одна.

Мы уже видели такие рисунки. Те самые рисунки, которые две тысячи лет назад использовали Архимед и Евдокс, когда разрабатывали метод исчерпывания. Последний рисунок похож на окружность с диаметром в одну единицу. Но на самом деле это многоугольник, состоящий из 65 536 крохотных иголок. Ваши глаза не заметят разницы, так же как не заметит ее и пол. Это означает, что ожидаемое количество пересечений окружности диаметром в одну единицу в точности такое же, что и ожидаемое количество пересечений 65536-угольника. А согласно правилу согнутой иглы, это количество равно Np , где N – это периметр многоугольника. Чему равен этот периметр? Он должен быть в точности таким же, что и длина окружности; радиус окружности равен 1/2 единицы, а значит, длина этой окружности равна π. Следовательно, ожидаемое количество пересечений окружности с краями планки равно π p .

Как вы воспринимаете такое усложнение задачи? Не кажется ли вам, что мы делаем задачу все более абстрактной и все более обобщенной, даже не ответив на основной вопрос: что такое p ?

Так вот, представьте себе: мы только что вычислили это значение.

Ведь вопрос теперь звучит так: сколько пересечений делает окружность? Совершенно неожиданно задача, казавшаяся сложной, становится простой. Симметрия, которую мы потеряли, когда перешли от круга к игле, восстановлена посредством сгибания иглы в кольцо. А это существенно упрощает задачу. Не имеет значения, куда упадет круг, – он пересекает линии на полу ровно два раза.

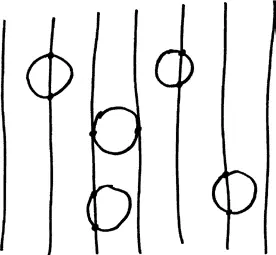
Таким образом, ожидаемое количество пересечений равно 2; оно же равно π p . Следовательно, мы можем сделать вывод, что p = 2 / π, как и говорил Бюффон. На самом деле представленная выше аргументация применима к любой игле, какой бы многосторонней или изогнутой она ни была: ожидаемое количество пересечений равно Lp , где L – это длина иглы в единицах, равных ширине планки. Бросьте на кафельный пол груду спагетти – и я смогу точно сказать, какое число пересечений линий с макаронинами следует ожидать. Математические остряки называют этот обобщенный вариант задачей Бюффона о лапше .

Доказательство Барбье напоминает мне слова Пьера Делиня, специалиста по алгебраической геометрии, сказанные им о своем учителе Александре Гротендике: «Кажется, будто ничего не происходит, и все-таки в итоге получается в высшей степени нетривиальная теорема» {169}.