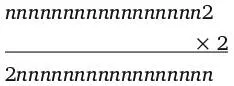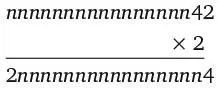Алекс Беллос - Капуста, неверные мужья и зебра. Загадки и головоломки для развития критического мышления

(1000 a + 100 b + 10 c + d ) × 4 = 1000 d + 100 c + 10 b + a.

Теперь нам предстоит найти правильные способы упрощения и решения этого уравнения.

Шаг 1. Определяем значение a.

Значение левой стороны уравнения четное, поскольку имеет множитель 4; следовательно, его правая сторона тоже должна быть четной. Левая сторона уравнения устанавливает предел значения a , поскольку 4000 a должно быть меньше 9999. (Если бы оно было больше 9999, в правой части уравнения было бы пятизначное число.) Единственное четное число, соответствующее этим условиям, – 2, поэтому a = 2.

Шаг 2. Определяем значение b.

Поскольку a = 2, левая сторона уравнения – это минимум 8000, а значит, значение d либо 8, либо 9. Однако если бы d = 9, в разряде единиц в левой части уравнения была бы цифра 6, так как 9 × 6 = 36. Но в разряде единиц должна быть цифра 2, потому что a = 2 правой части уравнения. Следовательно, d = 8.

Подставим эти значения в исходное уравнение:

(2000 + 100 b + 10 c +8) × 4 = 8000 + 100 c + 10 b + 2.

Это уравнение можно привести к такому виду:

8032 + 400 b + 40 c = 8002 + 100 c + 10 b.

А затем к такому

390 b + 30 = 60 c.

И далее

13 b + 1 = 2 c.

Не забывайте, что b и c – это отдельные цифры. Максимально возможное значение c = 9, а это значит, что максимально возможное значение 2 c = 18. Таким образом, b может иметь только значение 1. А если b = 1, то c = 7.

Следовательно, ответ – 2178, так как 2178 × 4 = 8712.

К тексту

Мы ищем такое число, при умножении которого на 2 последняя цифра произведения была бы первой цифрой полученного результата. Фримен Дайсон любезно сообщил нам о том, что минимальное число с таким свойством состоит из 18 цифр, поэтому обозначим его как nnnnnnnnnnnnnnnnnn R , где каждая n – это цифра, а n R – крайняя справа цифра.

Мы знаем, что

Найдем цифру для n R. Мы не можем взять 0, иначе ответ содержал бы всего 17 цифр, что делает умножение невозможным. Мы также не можем выбрать 1, потому что тогда ответ начинался бы с 1, что тоже невозможно: половина 18-значного числа, начинающегося с 1, – это 17-значное число, что противоречит условию задачи (исходное число состоит из 18 цифр). Возьмем 2.

И наше произведение становится таким:

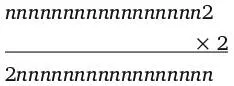
Это уравнение можно решить, определяя значения n. Поскольку 2 × 2 = 4, последней цифрой нижнего числа будет 4.

Нижнее число состоит из тех же цифр и в том же порядке, что и верхнее, за исключением того, что последняя цифра верхнего числа – первая цифра нижнего числа. Из этого следует, что первая цифра нижнего числа – это предпоследняя цифра верхнего числа. Таким образом, предпоследняя цифра верхнего числа – 4.

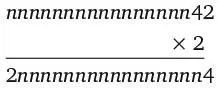
Поскольку 4 × 2 = 8, предпоследней цифрой нижнего числа, а значит, и третьей от конца цифрой верхнего числа должна быть цифра 8.

До сих пор мы выполняли только операцию умножения на два. Наше следующее значение – 8 × 2 = 16, поэтому на следующей позиции (третья цифра с конца нижнего числа и четвертая цифра с конца верхнего числа) должна быть цифра 6, но поскольку она взята из числа 16, то мы должны перенести 1.

Для следующего значения n у нас есть 6 × 2 = 12, но есть еще и перенос 1, что в сумме дает 13. Таким образом, на следующей позиции (четвертая от конца цифра нижнего числа и пятая от конца цифра верхнего числа) находится цифра 3, снова с переносом 1.

Продолжив умножение для нахождения обоих чисел, в итоге получим:

Итак, мы получили нужный ответ: произведение числа 105 263 157 894 736 842 на два представляет собой то же число, в котором последняя цифра становится первой.