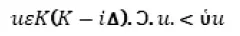Жюль Пуанкаре - Теорема века. Мир с точки зрения математики

Далее мы определили число N , правда, при помощи конечного числа слов, но мы опирались на понятие о совокупности Е . Вот почему N и не составляет части Е .

В примере, избранном Ришаром, вывод представляется с полной очевидностью, и очевидность эта станет еще более ясной, если обратиться к самому тексту письма. Но это же объяснение годится, как в том легко убедиться, и для других антиномий.

Итак, те определения, которые должны быть рассматриваемы как непредикативные, заключают ложный круг. Предшествовавшие примеры достаточно показали, что я под этим разумею. Не это ли Рассел обозначает названием «zigzagginess»?

Я ставлю вопрос, не разрешая его.

Рассмотрим теперь мнимые доказательства принципа индукции и в особенности доказательства Уайтхеда и Бурали-Форти. Поговорим сначала о доказательстве Уайтхеда и воспользуемся некоторыми новыми и удачными обозначениями, которые Рассел ввел в своем последнем мемуаре.

Назовем рекуррентным классом всякий класс чисел, который содержит 0 и который содержит n + 1, если он содержит n .

Назовем индуктивным числом всякое число, которое составляет часть всех рекуррентных классов.

При каком условии это последнее определение, играющее существенную роль в доказательстве Уайтхеда, будет «предикативным» и, следовательно, приемлемым?

Согласно предшествующему изложению под всеми рекуррентными классами надо понимать все классы, в определение которых не входит понятие об индуктивном числе.

Без этого можно впасть в ложный круг, который и породил антиномии.

Но Уайтхед не принял этой предосторожности.

Его рассуждение ложно; именно оно и повело к антиномиям; оно было незаконным, когда давало ложные результаты, и остается незаконным, когда приводит случайно к правильному результату.

Определение, которое содержит заколдованный круг, ничего не определяет. Не к чему говорить: мы уверены, что, какой бы смысл ни был дан нашему определению, все же существует по крайней мере нуль, который принадлежит классу индуктивных чисел. Дело не в том, чтобы узнать, пуст ли этот класс, а в том, чтобы его строго отграничить. «Непредикативный» класс – это не пустой класс, а класс, в котором граница оказывается неопределенной.

Излишне прибавлять, что это частное возражение оставляет в силе те общие возражения, которые приложимы ко всем доказательствам.

Второй гласит:

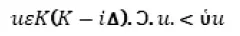
Первый постулат не более очевиден, чем принцип, подлежащий доказательству. Второй не только не очевиден, но и ложен, как это показал Уайтхед и как это, впрочем, заметил бы любой лицеист математического класса, если бы аксиома была выражена на понятном языке. Ибо эта аксиома означает: число комбинаций, которые можно образовать из нескольких предметов, менее числа этих предметов.

В известном доказательстве Цермело опирается на следующую аксиому:

В какой-либо совокупности (или даже в каждой из совокупностей некоторой совокупности совокупностей) мы можем всегда выбрать наудачу один элемент (даже тогда, когда эта совокупность совокупностей обнимает бесконечно много совокупностей). Тысячу раз применяли эту аксиому, не высказывая ее. Но лишь только она была высказана, как появились сомнения. Одни математики, как Борель, ее отвергают, другие восхищаются ею. Посмотрим, что об этом думает Рассел в своей последней статье.

Он не высказывается, но те размышления, которым он предается, очень знаменательны.

Однако сначала один наглядный пример. Допустим, что мы имеем столько пар сапог, сколько есть целых чисел, так что мы можем нумеровать пары от 1 до бесконечности. Сколько мы будем иметь сапог? Будет ли число сапог равно числу пар? Да, если в каждой паре правый сапог отличается от левого, ибо в таком случае достаточно будет обозначить номером 2 n − 1 правый сапог n -й пары, а номером 2 n – левый сапог n -й пары. Нет, если правый сапог подобен левому, так как в этом случае такая операция будет невозможна. Иначе придется допустить аксиому Цермело, потому что тогда можно в каждой паре выбрать наудачу сапог, который будет рассматриваться как правый.

Доказательство, действительно основанное па принципах аналитической логики, будет составляться из ряда предложений. Одни из них, которые служат посылками, будут тождествами или определениями; другие будут последовательно выведены из первых. Но, хотя связь между каждым предложением и последующим замечается непосредственно, трудно будет с первого взгляда увидеть, как мог совершиться переход от первого предложения к последнему, и явится соблазн рассматривать это последнее как новую истину. Но если последовательно заменить фигурирующие в нем различные выражения их определениями, если провести эту операцию насколько можно далеко, то в итоге останутся только тождества, так что все сведется к бесконечной тавтологии. Логика, следовательно, окажется бесплодной, если не будет оплодотворена интуицией.