Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Имперский геометр . Даже в самых глубоких ущельях неверия в собственные силы я был благодарен лорду Вейдеру за обратную связь. Он требовательный управленец, как и многие визионеры. Но я знаю, что все это было в рамках конструктивной критики.

Дарт Вейдер . Кретин.

Имперский геометр. В конце концов мы выявили единственный целевой показатель: симметрию.

Большинство людей небрежно пользуются этим термином, но в математике слово «симметрия» имеет точное определение: то, что можно сделать с фигурой, чтобы она выглядела так же, как раньше.

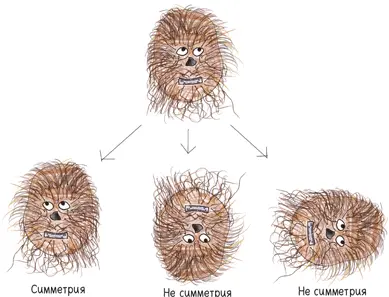
Например, морда вуки имеет одну-единственную симметрию: ее можно отразить в вертикальном зеркале {36} 36 Не обращайте внимания на направление взгляда вуки, только на форму морды. — Прим. науч. ред. . Вот и все. Если вы проделаете что-нибудь еще (скажем, повернете ее на 90° или отразите в горизонтальном зеркале), вы измените его морду до неузнаваемости, после чего вуки может попытаться изменить до неузнаваемости вашу физиономию.

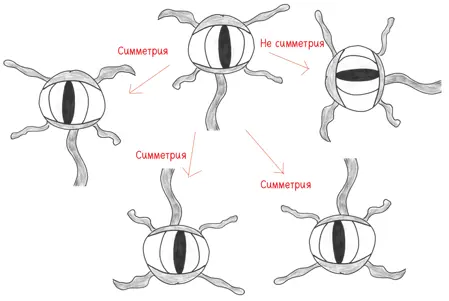
Напротив, морда дианоги [67] Благодарю Грегора Назариана, который смягчил мое сердце, как музыкальная тема Джона Уильямса, и помог существенно улучшить эту главу. (Я упоминаю его здесь, потому что он подсказал мне идею с дианогой, а не потому, что его лицо напоминает дианогу.) (болотной обитательницы с щупальцами, которая иногда заводится в мусорных контейнерах) обладает тремя симметриями: два отражения и поворот на 180° {37} 37 А тут не обращайте внимание на щупальца, иначе все будет как у вуки. — Прим. науч. ред. .

Гранд-мофф Таркин. Зачем зацикливаться на симметрии? Ну, симметрия — суть красоты.

Посмотрим, скажем, на человеческие лица. Ни одно не симметрично идеально. Одно ухо чуть повыше; один глаз чуть побольше; нос слегка кривоват. Но чем симметричнее лицо, тем красивее оно нам кажется. Странный психологический факт: математика — мерило красоты.

Мы стремились, чтобы «Звезда смерти» сражала наповал, как лицо супермодели.

Имперский геометр . Однажды лорд Вейдер смел мои чертежи со стола и зарычал: «БОЛЬШЕ СИММЕТРИИ!» Мы рассматривали икосаэдр, у которого 120 симметрий. Как я мог добиться большего? Но потом я все-таки нашел решение, и я больше всего горжусь этим моментом моей карьеры — нет, черт возьми, всей моей ЖИЗНИ. Я нашел решение: максимально симметричное геометрическое тело.

Дарт Вейдер. Почему ему сразу не пришло в голову начать с шара? Черепашья скорость немощных мозгов отнимает слишком много времени.

Гранд-мофф Таркин. Головная боль никуда не делась. Нам необходимо было установить набор лазеров, уничтожающих планеты, в северном полушарии «Звезды смерти» и тем самым нарушить симметрию. Нам это сильно попортило кровь.

Имперский геометр . Я по-прежнему убежден: монтировать этот лазер было ошибкой. Я имею в виду, что эффективнее для устрашения — небольшое лазерное шоу или БЕСКОНЕЧНОЕ число симметрий?

Гранд-мофф Таркин. Мы сразу же столкнулись с трудностью. Можно сказать, со встречным ветром.

Все бывали внутри «Звездных разрушителей» и помнят эти сверкающие угловатые конструкции. Они были галактическими ножами для стейков, готовыми вспороть любую звезду, как воздушный шарик с гелием. Когда я осознал, что дизайн должен быть не только эстетичным, но и функциональным, это доставило неприятности нашей станции.

Имперский физик . Представьте, что вы летите на аэроплане. Неважно, насколько вы хороший пилот, все равно вас ждет ЧРЕЗВЫЧАЙНО много столкновений. Я имею в виду, разумеется, столкновения с молекулами воздуха.

Наилучший сценарий? Молекулы воздуха скользят ПАРАЛЛЕЛЬНО поверхности вашего самолета. Таким образом, они никак не влияют на ваше движение. Они похожи на поток автомобилей на встречной полосе. Наихудший сценарий: молекулы воздуха двигаются ПЕРПЕНДИКУЛЯРНО поверхности самолета, под углом 90°. Тогда все молекулы в полной мере влияют на ваше движение. Вот почему вы не станете строить аэроплан с большой, плоской фронтальной поверхностью: он будет похож на человека-сэндвича с рекламными щитами, пробивающегося сквозь толпу.

Поэтому «Звездный разрушитель» имеет клиновидную форму. Когда он летит сквозь атмосферу, молекулы воздуха в основном скользят вдоль его бортов — почти параллельно поверхности. Напротив, «Звезда смерти» стала нашим аэродинамическим ночным кошмаром. Ее огромная поверхность вынуждена сталкиваться с молекулами воздуха под практически идеально прямым углом.