Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Чтобы понять, что я имею в виду, обратимся к запутанной истории теории узлов [13] Подробнее: Matthey Parker, Things to Make and Do in the Fourth Dimension. — London: Penguin Random House, 2014. [ Паркер М. Чем заняться в четвертом измерении? — М.: АСТ, 2020.] .

Эта отрасль математики, как и многие другие, была вдохновлена естественно-научной задачей. До открытия атомов некоторые ученые (включая лорда Кельвина) придерживались мнения, что вселенная наполнена субстанцией под названием «эфир», а материя создана из узлов и клубков эфира. Они стремились к тому, чтобы классифицировать все возможные узлы и создать периодическую таблицу клубков.

Вскоре физики утратили интерес к этой идее, поглощенные новой блестящей теорией атомов {13} 13 Планетарная модель атома, предложенная Эрнестом Резерфордом в 1911 году: электроны вращаются вокруг массивного ядра подобно тому, как планеты вращаются вокруг Солнца. — Прим. пер. (ее несправедливое преимущество заключалось в том, что она была верна {14} 14 Впрочем, вскорости оказалось, что и планетарная модель неверна, и она была заменена квантовой. — Прим. науч. ред . ). Но математики уже попались на крючок. Они обнаружили, что классификация узлов — сладостная и дьявольская задача. Две разновидности одного и того же узла могли выглядеть совершенно по-разному. Абсолютно отличающиеся друг от друга узлы поражали своим сходством. Это было отличной подпиткой для математиков, которые скоро разработали сложную и исчерпывающую теорию узлов, будучи уверены, что их интеллектуальная абстракция не имеет никакого практического применения.

Прошло около ста лет.

И вот из укрытия выползла настоящая змея. Как вы знаете, каждая биологическая клетка содержит информацию в молекуле ДНК, которая фантастически длинна. Если выпрямить ДНК одной клетки вашего организма, она растянется почти на два метра. В 100 000 раз длиннее самой клетки.

ДНК — это длинная струна, упакованная в миниатюрный контейнер. Если вы когда-нибудь клали наушники в карман или вынимали новогоднюю гирлянду из картонной коробки, вы знаете, что их необходимо свернуть в клубок. Как это удается бактерии? Можем ли мы выучиться у бактерии такому трюку? Можем ли обезвредить раковую клетку, расплетая ее ДНК?

Биология была в недоумении. Ей требовалась помощь. «О! — воскликнула математика. — Я знаю одну штуку!»

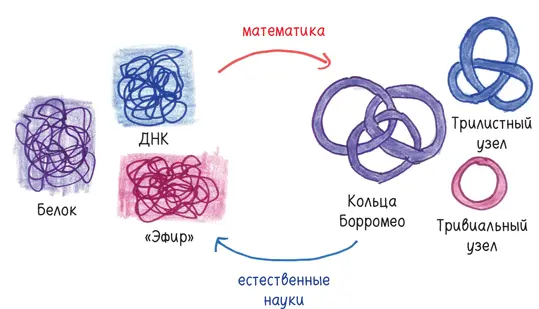
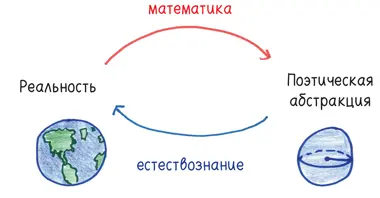
Вот краткая биография теории узлов {15} 15 Подробности можно прочесть в книге: Сосинский А. Узлы. Хронология одной математической теории. — М.: МЦНМО, 2005 ( http://files.school-collection.edu.ru/dlrstore/d63008f4-a780–11dc-945c-d34917fee0be/71_sosinskij_uzli.pdf ). — Прим. пер. . Она родилась из практических нужд. Вскоре она превратилась в нечто абсолютно оторванное от практики, логическую игру для поэтов и философов. А дальше каким-то образом это творение, которое на протяжении многих лет, казалось, не имело никакого отношения к реальной жизни, стало чрезвычайно полезным совершенно не в той области, ради которой оно родилось.

Это не единичный случай. Это обычная схема в истории математики.

Помните странную альтернативную геометрию, о которой шла речь в первой главе? На протяжении веков ученые рассматривали ее как фантазию, поэтическую прихоть. Они не видели соответствия с нашей реальностью, в которой, как предполагалось, действовал постулат Евклида о параллельных прямых.

Но в один прекрасный день на сцене появился молодой клерк из патентного бюро по фамилии Эйнштейн. Он понял, что безумная геометрия — не просто мысленный эксперимент; она определяет структуру космоса. С нашей ограниченной точки зрения, вселенная выглядит евклидовой, а шарообразная Земля — плоской. Но если изменить масштаб и отбросить предрассудки обитателя плоскости, откроется совершенно иная картина: переменчивый ландшафт поразительных изгибов [14] Я благодарен Мэтью Фрэнсису и Эндрю Стейси за помощь по этому вопросу. Я хотел написать, что Вселенная «гиперболическая» или «эллиптическая», а не «евклидова», но они сообщили мне, что в действительности она представляет собой труднопостигаемое лоскутное одеяло из этих более простых геометрий. Стейси написал: «Риманова геометрия обобщает евклидову во многих отношениях; она намного богаче евклидовой, но упускает из виду некоторые аспекты, в первую очередь то, как объекты соотносятся друг с другом в различных областях пространства». Это включает и понятие параллельных прямых. Фрэнсис добавил интересную историческую деталь: «В XIX веке Уильям Кингдон Клиффорд предложил использовать неевклидову геометрию, чтобы заменить физическое понятие силы, но он просто полагал, что „это было бы прикольно“. Меня не удивило бы, если другие тоже продумывали подобные идеи». Естественно, Эйнштейн тесно сотрудничал с математиками; ни один прорыв не происходит сам по себе. .