Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Альтернатива: распределять голоса выборщиков по географическому принципу. У вас есть десять выборщиков, почему бы не разбить ваш штат на десять избирательных округов и дать по одному голосу выборщика победителю в каждом округе?

Эта система пережила свой расцвет в 1790-е и начале 1800-х. С тех пор она канула в Лету.

Ее ближайший ныне действующий аналог — распределять голоса выборщиков в соответствии с избирательными округами на выборах в Палату представителей {78} . Затем, поскольку в каждом штате на два выборщика больше, чем делегатов от этого штата в Палате представителей, голоса двух оставшихся выборщиков достаются победителю по штату в целом.

Сегодня эта своеобразная система практикуется всего в двух штатах: Небраска и Мэн. И больше нигде.

Так что, черт возьми, происходит в других 48 штатах? Они следуют радикальной схеме: победитель забирает все. В соответствии с этим подходом победитель прямого голосования в целом по штату получает все голоса выборщиков.

Принцип «победитель забирает все» имеет внятный подтекст: неважно, насколько победитель опередил проигравшего. В 2000 году Джордж Буш одержал победу во Флориде с преимуществом менее чем в 600 голосов. Избираясь на второй срок, он получил преимущество в 400 000 голосов. Но грандиозный отрыв был для него ничем не лучше зазора тоньше волоса. Принцип «победитель забирает все» сводит непрерывное разнообразие возможного распределения голосов к двум дискретным результатам, чего не могли ни предусмотреть, ни предвидеть 55 умников в Филадельфии.

Почему же тогда этот принцип практикуется в 96 % штатов?

Эта проблема напрямую относится к теории игр, математическому выбору стратегии. Для того чтобы понять текущую ситуацию, нам нужно проникнуть в сознание политика уровня штата.

Начнем с Калифорнии. Демократы имеют преимущество в Законодательном собрании штата. И — сюрприз-сюрприз — демократы, как правило, получают больше голосов на президентских выборах. Представьте, что у вас есть два варианта: пропорциональное распределение голосов выборщиков или принцип «победитель забирает все».

Ну, если вы демократ, то этот принцип дает фору вашей партии. Идти каким-либо иным путем означает подарить горстку голосов республиканцам. Зачем вообще раздумывать на эту тему?

В Техасе действует та же логика, только другая цветовая гамма. Этот принцип обеспечивает все голоса выборщиков республиканцам. Зачем же уступать драгоценные голоса сопернику?

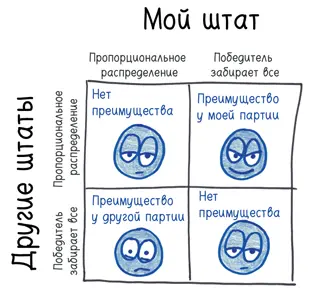
Теоретически, если бы голоса выборщиков распределялись пропорционально на основе прямого голосования, ни одна партия не получила бы преимущество. Как будто оба дуэлянта сложили оружие. (Левая верхняя клетка на диаграмме.)

Однако это отнюдь не устойчивое равновесие. Как только противник отбросит свой револьвер, вы тут же можете снова подобрать свой. Если все штаты следуют одному и тому же принципу, мы скоро оказываемся в нижней правой клетке диаграммы, где, разумеется, сегодня пребывают 96 % штатов [250].

По описанию Коллегии выборщиков у вас могло сложиться впечатление, что границы штата имеют значение. Что пользоваться одинаковыми водительскими правами означает состоять в особом родстве {79} . Но законодатели действуют иначе. Выбирая систему «все или ничего», они делают то, что лучше для партии, даже если это означает маргинализацию штата.

Например, вот итоги десяти последних выборов в Техасе:

Действовать по принципу «победитель забирает все» — это все равно что вывесить на границе штата огромный билборд: «Неважно, что думают местные избиратели: здесь всегда побеждают республиканцы!». В соответствии с ним 55 % ничем не хуже 85 %, а 45 % ничем не лучше 15 %. Этот принцип означает, что выборы заканчиваются, не успев начаться, и у обеих партий нет поводов подстраивать свою политику под интересы местных граждан, чтобы завоевать их голоса. Зачем тратить ресурсы, если это ничего не изменит?