Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Мы, американцы, верим в правительство, состоящее из граждан, сформированное гражданами и работающее ради граждан. Поэтому приходится краснеть из-за того, что люди, похоже, никогда не могут ни о чем договориться.

По-моему, достаточно сложно достичь семейного консенсуса даже при выборе пиццы. Тем не менее каким-то образом наша шумная демократия, удерживающая в напряжении целый континент, должна принимать однозначные коллективные решения по гораздо более существенным вопросам. Мы вступаем в войну — или нет. Мы избираем президента, того или иного. Мы заключаем болельщиков баскетбольного клуба «Лейкерс» в тюрьму — или позволяем им безнаказанно расхаживать по улицам. Как же нам удается объединить 300 млн голосов в один национальный хор?

Вообще, это требует некоторой технической работы. Провести перепись населения. Подсчитать голоса. Заполнить таблицы. Выяснить процентные соотношения. Эта вычислительная работа, пусть немного нудная, все же жизненно важна по той причине, что по сути своей представительная демократия — это математическое действо [243].

Простейшая демократическая система носит название «правило абсолютного большинства». Есть один-единственный переломный момент: рубеж проходит на уровне 50 %. Один дополнительный голос в вашу пользу может сделать вас победителем (или наоборот).

Но забудьте слово «просто». Это же Америка! Для выборов нашего президента мы сконструировали умопомрачительный механизм, известный под названием «Коллегия выборщиков» — математическая и политическая аномалия, подразумевающая десятки переломных моментов. Она не только подливает бензина в костер наших бесконечных дискуссий о «красных» и «синих» штатах, но и наделяет наши выборы завораживающими математическими свойствами. В этой главе я хочу проследить изгибы и повороты в истории Коллегии выборщиков:

1. Она начинается со слоя граждан.

2. Она становится слоем математики.

3. Она превратилась в систему, где победитель на уровне штата получает все голоса выборщиков в этом штате.

4. В конце концов она стала весьма похожа на прямое всенародное голосование — но с парой курьезных сюрпризов.

В итоге понимание Коллегии выборщиков сводится к вопросу предельного анализа. Что значит один шаг в марше 300-миллионной толпы под названием «американская демократия»?

Летом 1787 года в Филадельфии 55 щеголей, нахлобучив парики, ежедневно собирались, чтобы отчеканить план новой формы государственного управления. В наши дни мы называем их проект «Конституцией», и она наряду с чизбургером лежит в основе нашего национального характера.

Конституция закрепляет избирательную систему, позволяющую определить, кто станет президентом (в переводе с латыни — «сидящим во главе стола»). Каждые четыре года его избирают особые выборщики — «люди, избранные народом для определенной цели на определенный срок» [244]. Я воспринимаю выборщиков как временный комитет, выбирающий гендиректора компании. Они собираются с одной-единственной целью, выбирают нового лидера нации, а затем расходятся.

Откуда берутся выборщики? Из штатов. Каждый штат выбирает столько же выборщиков, сколько конгрессменов, и может выбирать их любым приглянувшимся методом.

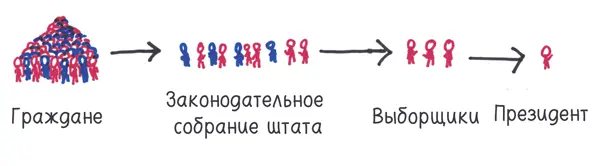
Логика заключалась в том, что местные избиратели знали только местных политиков. Времена тогда царили темные, до пришествия хештегов оставалось больше двух столетий, и разве народ мог судить об ораторском искусстве и модных прическах далеких незнакомцев? Поэтому Коллегия выборщиков процеживала предпочтения избирателей через три сита: во-первых, вы голосуете за местного представителя вашего штата; во-вторых, представители штата избирают выборщиков (или создают систему их избрания); в-третьих, выборщики избирают президента.

Однако к 1832 году все штаты, за исключением Южной Каролины, швырнули своих выборщиков в горнило демократической борьбы и предоставили гражданам решать самостоятельно [245].