Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Что изменилось?

Пятьдесят пять джентльменов в Филадельфии {77} воображали себе просвещенную демократию совестливых государственных мужей, не обремененных мерзкими дрязгами соперничества под названием «политические партии». Затем они разбрелись и создали нечто чертовски похожее на политические партии.

Не будем лицемерить: эта система имела свои преимущества. Теперь отпала необходимость рассматривать под лупой пятна на совести каждого отдельно взятого кандидата. Можно просто ознакомиться с партийными программами и отдать свой голос за команду, которая пришлась вам по душе. Нет необходимости в посредниках.

И вот страна перешла от выборщиков из плоти и крови к абстрактным голосам выборщиков, слой государственных деятелей сменился слоем математики.

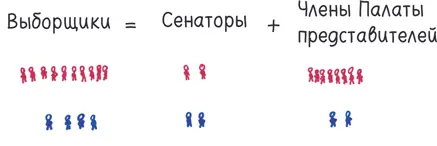
Конечно же, как и во многих составляющих Конституции, в этой системе было закодировано преимущество для рабовладельцев [246]. Как функционировал этот механизм? Вспомните, что каждый штат делегировал столько же выборщиков, сколько конгрессменов, то есть сенаторов (по два от каждого штата) и членов Палаты представителей (их число было прямо пропорционально численности населения и в 1804 году варьировалось от 1 до 22 от того или иного штата).

Сенаторская составляющая этой формулы обеспечивала поддержку малых штатов, уравнивая в правах скромный Род-Айленд (меньше 100 000 жителей в те годы) и огромный Массачусетс (более 400 000 жителей). Но подлинные перипетии сюжета разворачивались в Палате представителей. Пятьдесят пять модников в Филадельфии спорили о том, следует ли при распределении мест в Палате представителей учитывать, сколько рабов проживает в том или ином штате. Если да, то рабовладельческий Юг получит дополнительных представителей; если нет, преимущество останется за Севером.

Они пошли на компромисс и приняли половинчатое решение. Каждый раб считался за 3/ 5человека. Позорнейшая дробь в истории юриспруденции.

Коллегия выборщиков перенесла этот выступающий за сохранение рабства компромисс в систему президентских выборов, как вирус, скачанный из приложения к электронному письму. Вот распределение выборщиков в 1800 году и сравнение с гипотетической системой, где рабы не учитывались вовсе [247]:

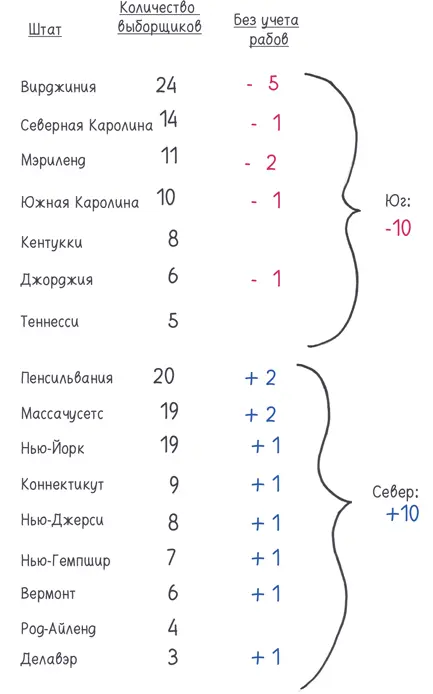
Возможно, вам кажется, что десять выборщиков — это мало. На самом деле это много. 32 года из первых 36 лет истории нашей страны во главе государства стояли представители рабовладельческой Вирджинии. Единственное исключение составил Джон Адамс из Массачусетса, который не был переизбран в 1800 году… На самом деле он был так близок к победе, что эти десять выборщиков сыграли свою роль.

В инаугурационной речи после тех горьких выборов 1800 года Томас Джефферсон взял примирительную ноту. Он сказал, что обе партии объединяют общие принципы, общие мечты. «Мы все федералисты, — сказал он. — Мы все республиканцы».

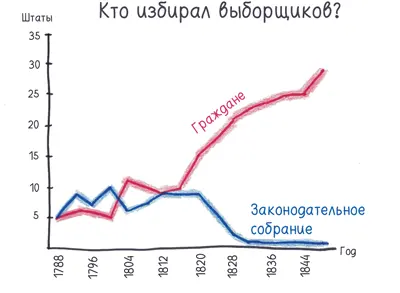
Однако посмотрите на Коллегию выборщиков в наши дни. Вы не увидите страну, которая гармонична, как инь и ян, и мирно хором распевает «Кумбайю». Карта пестрит красно-синим [248]. Калифорния безраздельно принадлежит демократам. Техас — республиканцам. Нет никакого «мы», исключительно «свои» и «чужие», что-то вроде настольной игры на двоих с невероятно высокими ставками.

Как же Коллегия выборщиков оказалась в таком положении?

Вот тут навострит уши математик. Конечно, мы позволим людям голосовать, но как объединить эти голоса и занести в таблицы? Какой математический процесс преобразует индивидуальные предпочтения в окончательный выбор избирателей?

Допустим, вы штат Миннесота. Вам нужно перемолоть три миллиона голосов граждан и получить на выходе десять голосов выборщиков. Как вы поступите?

Один из вариантов: распределить голоса выборщиков пропорциональнорезультатам прямого голосования граждан. Кандидат, набравший 60 %, получает шесть голосов выборщиков [249]. Кандидат, набравший 20 %, получает два голоса. И так далее.

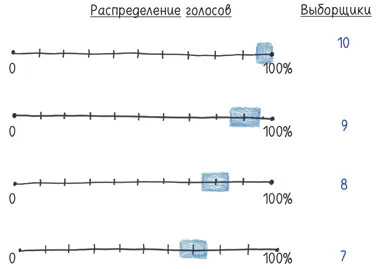
Хотя эта система логична, она не получила развития. На заре демократии отдельные штаты пробовали разные запутанные методы, например в Теннесси граждане избирали делегатов от своего административного округа, которые избирали выборщиков, которые избирали президента, но никто не видел необходимости распределять голоса пропорционально.