Джозеф Мазур - Игра случая. Математика и мифология совпадения

Линкольн рассказал о своем сне, в котором услышал плакальщиков и вышел из своей спальни, чтобы выяснить, откуда раздавались их рыдания. Скорбящие были невидимы, а звуки были повсюду. Когда он вошел в Восточный зал, то увидел труп на катафалке, окруженном почетным караулом и группой скорбящих. Ему сказали, что президент убит.

У Линкольна было много пророческих сновидений. Когда началась война, он видел тот же самый сон перед каждым важным для страны событием. Были ли они совпадениями или просто понятными переживаниями, связанными с неопределенностью, всплывающими через бессознательное, особенно в состоянии сна?

Сон Линкольна о собственном убийстве мог быть просто осознанием неопределенности его положения. До этого ни одного из президентов США не убивали, но это не значит, что он не думал о такой опасности, особенно во время войны. Как большинство снов, вещие также встроены в механизм сновидения; мы все равно «думаем», пока спим, или «думаем», что спим.

Джоан Гинтер 4 раза выиграла в лотерею. Она выиграла $5,4 млн в первый раз, $2 млн – во второй, $3 млн – в третий раз и $10 млн – в четвертый. Ее выигрыши растянулись на период в 18 лет начиная с 1993 г. Я признаю, что шансы подобного сочетания событий ничтожны, но не равны нулю. Технически ее история – не совпадение. У совпадений нет очевидных причин. У истории Гинтер есть очевидная причина: она выбрала выигрышные номера, покупая билеты оптом. Мы могли бы подумать, что ее 4 выигрыша в лотерею были колоссальной удачей. Что ж, мы были бы правы. Такие многократные выигрыши в самом деле редки. Но имеются скрытые факторы.

Во-первых, первый выигрыш принес ей легкие деньги, которые она использовала, чтобы играть снова и снова, каждый раз используя убытки от игры для покрытия части долга по налогам. Умно, но то же самое делают 80 % тех, кто взял джекпот: играют снова и снова, надеясь на следующую волну. В психологии теории игр такую волну называют подкреплением благоприятной истории {117}. А когда вы выиграли джекпот, вы ведь не покупаете один-два билета; вы покупаете их сотнями, даже тысячами. Но как выбирают выигрышные числа?

Мне сообщали, что шансы выбрать 4 выигрышных числа составляют 18 септиллионов к 1, а это настолько маловероятно, что может произойти с одним человеком только раз в квадриллион лет {118}. (Смотри описание хода вычислений в главе 7.) Может быть, и так, но, не зная, сколько раз Гинтер проиграла (а у нас нет возможности это узнать), нельзя выяснить действительные шансы. Некоторые части истории отсутствуют. У нее действительно есть докторская степень по математике, полученная в Стэнфорде, так что, возможно, для определения выигрышных номеров при покупке билетов оптом она использовала некий алгоритм.

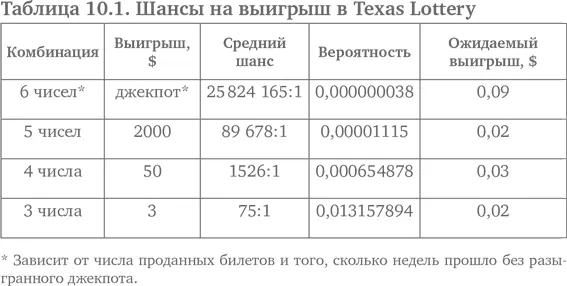
Давайте рассмотрим лотерею Texas Lotto. Игроки покупают один билет за $1 и отмечают 6 чисел от 1 до 54. Лотерея публикует шансы на выигрыш в таком виде, как показано в табл. 10.1. Предположим, что Гинтер купила один билет за $1 и выбрала 6 выигрышных чисел. При джекпоте $2 млн ожидаемый выигрыш составляет всего 9 центов с доллара. Можно выиграть три других приза, не составляющих джекпот, так что мы должны прибавить ожидаемое значение 7 центов (полный выигрыш, исключая джекпот) к ожидаемому значению джекпота, изменив таким образом ожидаемое значение выигрыша любого из призов на 16 центов. На каждый сыгранный доллар игрок выбрасывает 84 цента.

Кроме того, существуют налоги и вероятность разделить выигрыш с кем-то из игроков, поэтому ожидаемое значение сокращается примерно до 12 центов. Пул игроков увеличивается с размером джекпота, поэтому вероятность, что джекпот придется разделить между несколькими игроками, также растет.

Да, выиграть в лотерею 4 раза – колоссальная удача. Вероятность даже одного выигрыша поразительно мала. Четыре выигрыша Гинтер – событие с настолько малой вероятностью, что после запятой понадобится поставить 32 нуля, прежде чем начнут появляться числа, от нуля отличные. Но только потому, что мы называем конкретного человека в качестве четырехкратного победителя – Джоан Гинтер. Конечно, у нее столько же шансов выиграть любое число раз, пусть даже один раз, сколько имеется их у любого другого при условии, что она покупает только один билет за раз. Но шансы того, что кто-то выиграет джекпот, достаточно высоки, учитывая, что в год продается до 1 млрд билетов Texas Lotto. Все-таки кто-то выигрывает, хотя может пройти несколько розыгрышей, прежде чем появится победитель. В 2014 г. около 31 818 182 человек в США потратили $70 млрд на покупку лотерейных билетов. Если каждый год покупается 70 млрд билетов и если числа выбраны случайно (они не абсолютно случайные, как мы отметили в главе 6), тогда в течение года кто-то точно должен выиграть, и есть неплохие шансы того, что кто-то выиграет в течение месяца.