Джозеф Мазур - Игра случая. Математика и мифология совпадения

p ( 23 ) = 365/365 × 364/365 × 363/365 × … × 343/365 = (1/365)²³ × (365 × 364 × 363 ×… × 343) = 0,4927

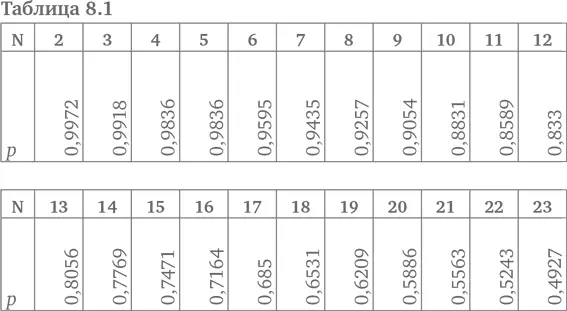
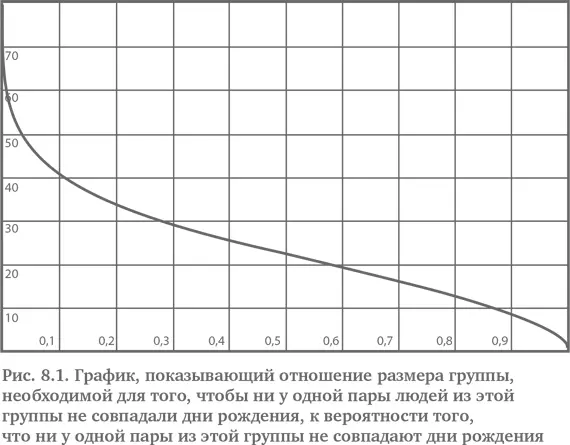
Таблица 8.1 и рис. 8.1 показывают, что p (23) (вероятность того, что у двух людей в группе из 23 человек совпадают дни рождения) равняется 0,4927. Переведем отрицание в утверждение и найдем вероятность того, что у 2 людей в группе из 23 человек совпадают дни рождения, равной 0,5073 – шанс выше, чем 1 к 1.

Даже при такой аккуратной формулировке в задаче есть допущения, которые могут исказить решение. Меньшим из допущений было не принимать в расчет високосные годы. Гораздо большим допущением было игнорирование того факта, что дни рождения не распределяются по календарю в случайном порядке, как нам может казаться. Мы знаем, что дни рождения склонны образовывать скопления по причинам, связанным с праздниками, природными катаклизмами, временами года и другими непостижимыми диспропорциями.

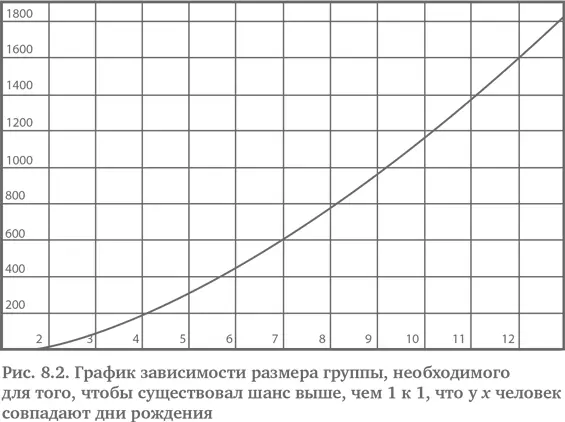
Есть несколько любопытных моментов. Чтобы иметь шансы выше, чем 1 к 1, что у 3 человек совпадают дни рождения, можно подумать, что потребуется еще примерно 23 человека. Верное число – 88. Для 4 совпадающих дней рождения это число становится уже 187 {83}. Таблицы 8.2 и рис. 8.2 показывают, как растут числа, где k представляет число совпадающих дней рождения {84}.

Стандартная задача о дне рождения была предложена Рихардом Мизесом, урожденным галичанином, который в 1933 г. предусмотрительно покинул Берлин и занял пост в Стамбульском университете, где проделал отличную работу в области механики жидких сред, аэродинамики и теории вероятностей. В 1939 г. он приехал в США, где занял должность в Гарварде {85}.

Задача эта многогранна. С одной стороны, это задача комбинаторики. Мы даже можем рассматривать ее как сугубо гипотетическую задачу об игральных костях: вы бросаете игральную кость с 365 сторонами 23 раза и находите вероятность того, что она дважды выпадет одной стороной. (Это гипотетический мысленный эксперимент, потому что реальной «правильной» игральной кости с 365 гранями не существует.) С другой стороны, можно пронумеровать все дни в году и перемешать, получив случайный набор чисел. Можно напечатать числа от 1 до 365 на пластиковых фишках, поместить во вращающийся барабан и выбирать по одной фишке N раз, не возвращая их назад в барабан. А потом спросим: какова вероятность p ( N ) того, что это число будет получено после N отборов {86}?

Если мы слегка изменим задачу и рассмотрим ситуацию, когда люди встречаются, скажем, на национальной конференции, то у скольких из них могут совпасть последние 4 цифры в номере социального страхования? Задача похожа на описанную выше. Единственным отличием будет то, что число 365 меняется на 9999, учитывая предположение о том, что ни у кого нет номера, заканчивающегося на 0000. С учетом этого предположения существует шанс выше, чем 1 к 1, что на конференции со 118 участниками у 2 из них совпадут последние 4 цифры номера социального страхования {87}.

Эти последние 4 цифры не имеют никакой закономерности и практически независимы от даты рождения владельца.

Непосредственно перед тем, как я начал писать эту книгу, Агнесс, соавтор онлайн-журнала для женщин, как-то узнала о том, что я работаю над книгой о совпадениях. «Уважаемый профессор Мазур, я прошу прощения, мой вопрос может показаться странным, – пишет она мне на электронную почту. – Насколько вероятно встретить человека (встретить лично, не в результате поиска через Интернет), у которого та же дата рождения, что и у вас (день, месяц и год)? Со мной это произошло дважды, по иронии судьбы в знаменательные моменты моей жизни».

До этого момента я никогда не задумывался над этим сложным вопросом. Однако по зрелом размышлении я быстро пришел к заключению, что его анализ дает нам математический аппарат практически для любого совпадения. Агнес спрашивает не о вероятности того, что у любых двух человек в группе совпадают дни рождения; напротив, она спрашивает о вероятности того, что у нее самой совпадает дата рождения с кем-то из группы, а на этот вопрос ответить куда сложнее. Для того чтобы выделить вопрос Агнесс, назовем его задачей о дате рождения .