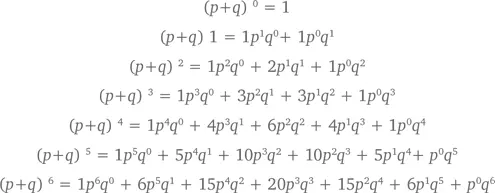Джозеф Мазур - Игра случая. Математика и мифология совпадения

Если мы возведем в степень n = 1, 2, 3, 4, 5, 6…, получим следующую матрицу в форме треугольника:

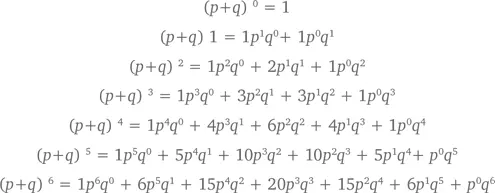
Для любого n константы в разложении двучленов ( p + q ) n – это как раз числа из треугольника Паскаля.

История этого треугольника начинается задолго до Блеза Паскаля {68}. Он в 1527 г. появился в работах китайского алгебраиста XIII в. Чу Шикей, позже – на титульном листе «Учебника по арифметике» Петера Апиана (который можно увидеть на картине «Послы» [1533 г.] работы Ганса Гольбейна-младшего), больше чем за век до того, как Паскаль исследовал треугольник, названный его именем {69}. В современном Иране треугольник известен как треугольник Хайяма, в честь известного персидского поэта и математика Омара Хайяма, который использовал треугольник в XII в., чтобы создать метод нахождения корней n -х степеней. В современном Китае он называется треугольником Ян Хуэя, в честь другого математика, который описал его в XIII в. В Италии это треугольник Тарталья, в честь математика Никколо Тарталья, жившего за век до Паскаля. Однако Паскаль, собрав уже известные наработки о треугольнике, использовал их в теории вероятностей {70}.

На рис. 7.2 показана вероятность выигрыша при ставке на «красное» в 100 турах рулетки. Мы уже видели, какую форму принимает график, когда рассматривали примеры вычислений в табл. 7.1 и коэффициенты, получаемые в результате разложения двучленов ( p + q ) n . Распределение столбцов на графике справедливо называют биномиальным распределением . Слово « биномиальное» происходит от конструкции, основанной на двух мономах p и q . По мере увеличения n график выравнивается и принимает форму колокола. Чем больше n , тем плавнее кривая.

Выберем некоторое большое значение n . Мы изменим гистограмму, сохранив без изменений ее площадь, а следовательно, и вероятность. Поскольку основание каждого столбца [11]имеет ширину в одно деление, распределение вероятностей представлено в виде площадей прямоугольников, а также их высотами. Некоторые разумные изменения – сдвиг, сжатие и растяжение – дают нам новый график, который сохраняет всю полезную информацию оригинала {71}. Конечно, теперь, в измененном графике, вертикальная ось уже не обозначает вероятность. Вероятность заключена в площадях прямоугольников, а эти площади не изменялись, потому что мы растянули график по вертикали и сжали по горизонтали в одной пропорции [12].

Чего мы достигли? Вот оно – чудо, вдохновенная идея. Кривую (гистограмма биномиального распределения, показанная на рис. 7.2), которая изображает вероятность выигрыша при ставке на «красное» в 100 турах рулетки, можно близко аппроксимировать к одной определенной математической кривой. Тут важно понимать, что одна эта кривая описывает великое множество природных феноменов, являющихся результатами случайностей. Поразительно, но эта кривая моделирует события рулетки, хотя и не имеет очевидной связи с шариками, падающими в красные ячейки колеса рулетки. Еще более удивительно, что та же кривая моделирует также и орлянку. Всего одна кривая описывает вероятности столь различных явлений. Чтобы получить информацию о вероятности конкретного явления, нам нужно ввести некоторые данные в модель. Мы должны предоставить два числа – среднее (среднее значение) и стандартное отклонение (мера разброса от среднего) {72}. Два этих числа дают информацию для модели, скажем, о рулетке, а именно: вероятность наступления события p (шарик падает в красную ячейку) – 9/19. Как только у нас есть эти конкретные p и N (число сыгранных туров рулетки), мы можем вычислить стандартное отклонение для нашей конкретной игры – ставки на «красное» в рулетке {73}. Это мера того, насколько велик разброс исходов от среднего, или стандартное отклонение от среднего , чаще называемое просто стандартным отклонением {74}.

Итак, каждая кривая биномиального распределения трансформируется с помощью математического трюка (посредством сдвигов и масштабирования) в особую могущественную кривую нормального распределения , график которой изображен на рис. 7.4 {75}.

Числа в основании кривой на рис. 7.4 – это стандартные отклонения от среднего. Мы объединили испытания в группы по стандартному отклонению. Отдельные вероятности исходов событий теперь не видны. Переменная X под кривой на рис. 7.4 показывает отклонение числа эмпирических успешных исходов от наиболее вероятного их числа. Иными словами, X , переменная горизонтальной оси, измеряется в стандартных отклонениях. Высота кривой – это уже не вероятность, поскольку мы ее масштабировали и сжали, сохранив площадь под кривой. Но в обмен на это масштабирование и сжатие мы получаем некоторые ценные сведения. Первое: около 68 % площади под кривой лежат на одном стандартном отклонении от среднего и около 95 % площади – на двух стандартных отклонениях от среднего. Второе: одно стандартное отклонение отмечено точками перегиба, т. е. точками на кривой, где кривая меняет форму с вогнутой на выпуклую.