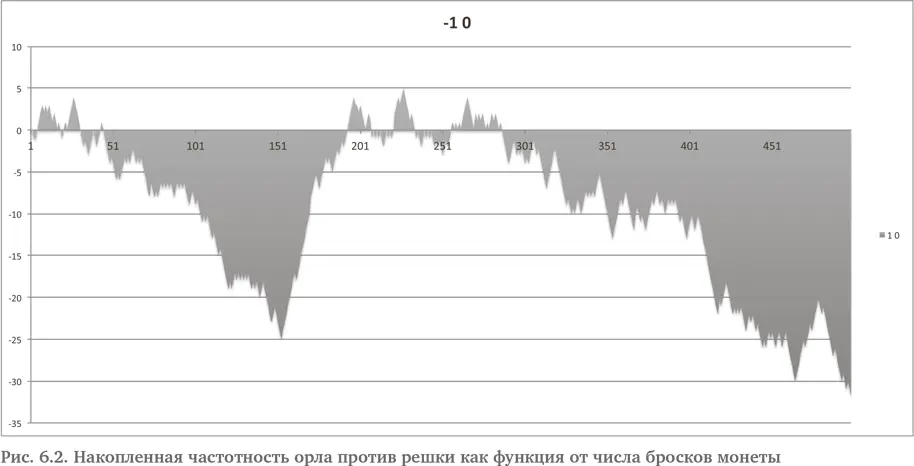
На рис. 6.2 мы увидим странную историю. Исходы вполне следуют ожиданиям вплоть до 45-го броска, когда решка вдруг перехватывает инициативу примерно на 105 следующих бросков! Затем идет достаточно долгий период, когда лидирует орел, и совокупное значение опять приближается к 0. Но около 286 броска решка опять надолго вырывается вперед. Не то чтобы события не согласовывались с нашими интуитивными ожиданиями. Действительное отношение орлов к решкам наверняка приблизится к 1 в ходе значительно более долгого времени, но в краткосрочной перспективе этого не происходит. За 500 бросков решка выпала только на 12 раз больше, чем орел. Это достаточно мало, но последовательности орлов и решек могут расходиться значительно сильнее в совокупных результатах. Например, рассмотрим следующее испытание, показанное на рис. 6.3.
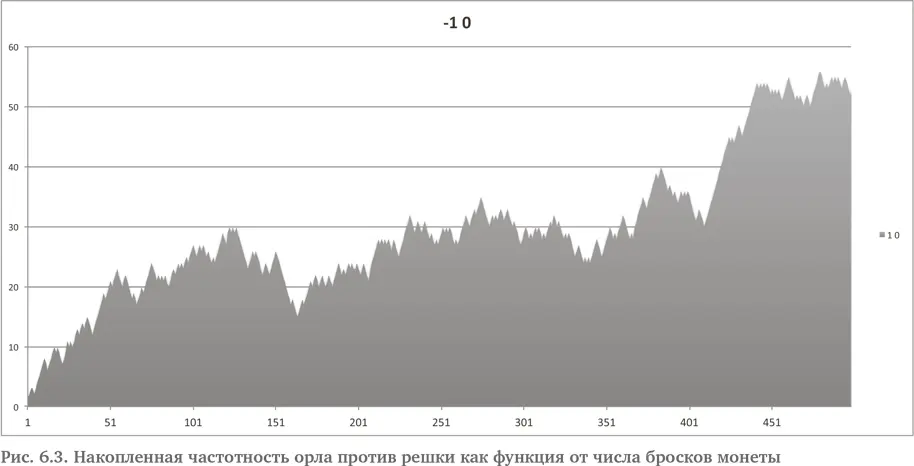
Орел полностью контролирует ситуацию. Совокупный исход показывает, что орел ведет настолько уверенно на протяжении всей серии бросков, что кажется, будто решка никогда уже не вырвется вперед.
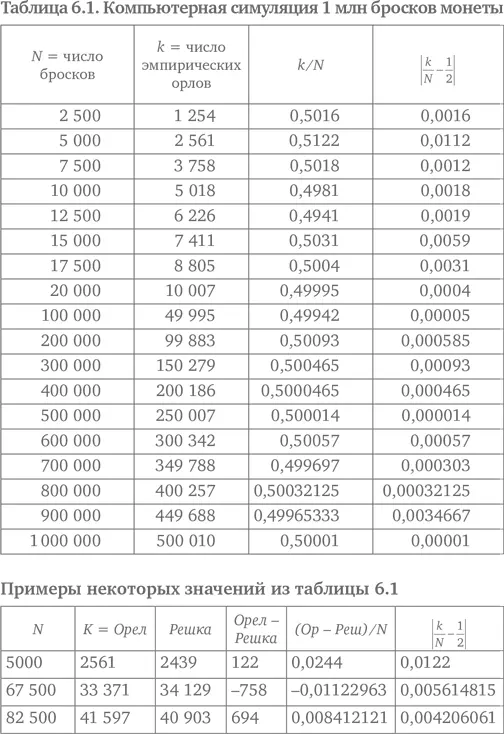
Результаты компьютерной модели 1 млн бросков разобраны в табл. 6.1. Отношение k / N , где k – число успешных исходов, а N – число испытаний, называют эмпирической частотой успешности испытаний . В правой колонке в табл. 6.1 приведены абсолютные значения разности между эмпирической частотой успешности испытаний и 1/2 – математически предсказанной частотой успешности испытаний.
Слабый закон больших чисел не исключает, что какие-то маловероятные события будут происходить часто на раннем этапе игры или на более поздних. На самом деле, даже если коэффициент успешности приближается к математически предсказанному, нет гарантии, что он таким и останется. Чуть более сильный математический результат говорит нам, что, хотя коэффициент успешности может сходиться к теоретически вычисленному, действительные значения коэффициента склонны к довольно странному поведению по мере увеличения числа испытаний. Контринтуитивно, но это так.
Слабый закон больших чисел, примененный к любому событию, вероятность которого равна p , говорит нам, что вероятность 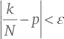 приближается к 1 по мере увеличения N . Возьмем ԑ = 0,0001 (выбрано произвольно) с p = 1/2 для ситуации с бросанием монеты и спросим, насколько возможно, что
приближается к 1 по мере увеличения N . Возьмем ԑ = 0,0001 (выбрано произвольно) с p = 1/2 для ситуации с бросанием монеты и спросим, насколько возможно, что 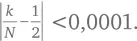 Обратите внимание (табл. 6.1), что
Обратите внимание (табл. 6.1), что 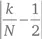 имеет резкие перепады при низких значениях N . Но они, очевидно, есть также и при высоких значениях. От 100 000 до 200 000 оно увеличивается. Даже с 800 000 до 900 000 оно увеличивается, пока не падает на миллионе. Создается обманчивое впечатление, что разность между орлом и решкой приближается к нулю. Но ничего не говорится о волатильности этого приближения при увеличении числа испытаний. Как мы видим, волатильность увеличивается по мере увеличения числа бросков монеты.
имеет резкие перепады при низких значениях N . Но они, очевидно, есть также и при высоких значениях. От 100 000 до 200 000 оно увеличивается. Даже с 800 000 до 900 000 оно увеличивается, пока не падает на миллионе. Создается обманчивое впечатление, что разность между орлом и решкой приближается к нулю. Но ничего не говорится о волатильности этого приближения при увеличении числа испытаний. Как мы видим, волатильность увеличивается по мере увеличения числа бросков монеты.
Итак, что же здесь происходит? Похоже, что у более высокого N есть некоторая свобода от закона больших чисел, поскольку в масштабах больших чисел больше места для незаметных ошибок.
Для 5000 бросков были 2561 орел и 2439 решек с разностью 122. Это дает ошибку в 2,4 %, что не так уж плохо. Но, если не знать распределение этих орлов, может случиться так, что 122 орла были выброшены последовательно. Придерживаясь этой точки зрения, представьте, что 758 решек выброшены последовательно за 67 500 бросков или 694 орла выброшены последовательно за 82 500 бросков. Другими словами, нет математического закона, который исключает возможность последовательного выпадения огромного числа орлов при большом N .
Глава 7
Треугольник Паскаля
В физическом мире не существует совершенной симметрии, искусственных машин с бесконечно малым допуском или идеальных моделей. Это мир множества скрытых переменных, явления которого слишком трудно охватить точной мерой. Иными словами, подлинные случайности действительно происходят, и мы часто обращаемся к вероятностным картинам событий, чтобы понять сложный феномен случайности.
Читать дальше
Конец ознакомительного отрывка
Купить книгу



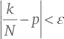 приближается к 1 по мере увеличения N . Возьмем ԑ = 0,0001 (выбрано произвольно) с p = 1/2 для ситуации с бросанием монеты и спросим, насколько возможно, что
приближается к 1 по мере увеличения N . Возьмем ԑ = 0,0001 (выбрано произвольно) с p = 1/2 для ситуации с бросанием монеты и спросим, насколько возможно, что 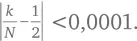 Обратите внимание (табл. 6.1), что
Обратите внимание (табл. 6.1), что 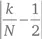 имеет резкие перепады при низких значениях N . Но они, очевидно, есть также и при высоких значениях. От 100 000 до 200 000 оно увеличивается. Даже с 800 000 до 900 000 оно увеличивается, пока не падает на миллионе. Создается обманчивое впечатление, что разность между орлом и решкой приближается к нулю. Но ничего не говорится о волатильности этого приближения при увеличении числа испытаний. Как мы видим, волатильность увеличивается по мере увеличения числа бросков монеты.
имеет резкие перепады при низких значениях N . Но они, очевидно, есть также и при высоких значениях. От 100 000 до 200 000 оно увеличивается. Даже с 800 000 до 900 000 оно увеличивается, пока не падает на миллионе. Создается обманчивое впечатление, что разность между орлом и решкой приближается к нулю. Но ничего не говорится о волатильности этого приближения при увеличении числа испытаний. Как мы видим, волатильность увеличивается по мере увеличения числа бросков монеты.










