На вопрос о пользе теоремы ответить несложно. Она решает классическую проблему геометрии большой теоретической важности. Таким образом, не говоря о практической пользе, важность ее состоит в том, что она служит основой множества теорем в тригонометрии и аналитической геометрии и, очевидно, в том, что она необходима для извлечения квадратных корней. Как мы увидим далее, проблема извлечения корней из чисел проявляется в достаточно простых математических задачах, таких как вычисление длины диагонали квадрата или прямоугольника по его сторонам.
Возможно, своим влиянием и известностью эта теорема обязана ощущению неочевидности, которое остается после ее анализа. В отличие от других теорем, в этой нет ничего интуитивно понятного, что объясняло бы ее свойства, которые мы сейчас еще раз рассмотрим, так что ее понимание — это акт чисто логической дедукции. Именно поэтому некоторые считают теорему квинтэссенцией математики.
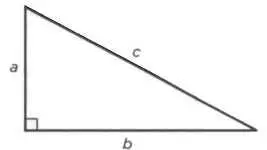
КАТЕТЫ, ГИПОТЕНУЗА И УГЛЫ
Катеты — это стороны, прилегающие к прямому углу прямоугольного треугольника, а гипотенуза — сторона, противоположная прямому углу. Термины эти пришли к нам из греческого языка. Слово «катет» восходит к древнегреческому kathetos, что значит «прямостоящий, перпендикулярный», а «гипотенуза» происходит от hypoteinousa — «натянутая, стягивающая». Это определение обозначает, что гипотенуза представляет собой диаметр окружности, на которой лежит вершина прямого угла прямоугольного треугольника, то есть диаметр, который «стягивает» прямой угол. Поскольку речь идет об углах, возможно, источник этих терминов — наблюдения над положениями мышц ноги или плеча и предплечья.
ОПРЕДЕЛЕНИЕ ТЕОРЕМЫ
Самое значительное открытие, которое традиция приписывает Пифагору, — это описание прямоугольного треугольника, устанавливающее соотношение между его катетами и гипотенузой. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов длин двух других сторон треугольника (см. рисунок 1). Определение теоремы звучит как «сумма квадратов катетов равна квадрату гипотенузы», а ее алгебраическое выражение выглядит так:
a 2+ b 2= c 2.
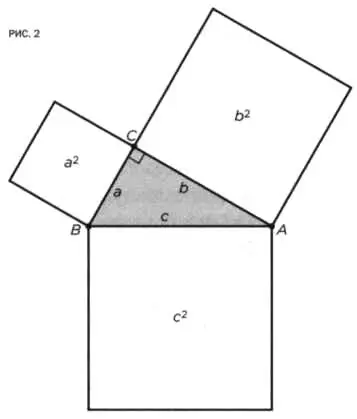
Эту теорему можно сформулировать и более строгим образом, следуя современным математическим нормам. Ее определение в специальных геометрических терминах выражается следующим образом (см. рисунок 2):
Дан треугольник ABC; угол С прямой (то есть треугольник является прямоугольным), если площадь квадрата, построенного на стороне с, противоположной углу С, равна сумме площадей квадратов, построенных на двух других сторонах a и b: a 2+ b 2= c 2.
Из уравнения а 2+ b 2= с 2следует, что
а = √(с 2-b 2),
b = √(с 2-а 2),
c = √(a 2+ b 2).
Во времена Пифагора эта теорема служила для определения перпендикулярности. Ведь в прямоугольном треугольнике «квадрат гипотенузы равен сумме квадратов катетов», потому что катеты перпендикулярны друг другу. С другой стороны, если на практике соотношение сторон именно таково (а 2+ b 2= с 2), отсюда можно вывести, что данный треугольник — прямоугольный.
В наши дни угольник и копировальная бумага, которые применяются для построения технических чертежей, позволяют проводить не только перпендикулярные отрезки, но и комбинировать углы их пересечения из углов в 30°, 45°, 60° и 90°. В современном мире при черчении с применением плотницкого или столярного угольника тем же инструментом можно проверять перпендикулярность линий. А в Древней Греции архитектор, желающий проверить, перпендикулярны ли друг другу стены, мог использовать теорему Пифагора. Инструментом для измерения длины в то время служила веревка с завязанными на равных расстояниях узелками. Этой веревкой архитектор отмерял 3 единицы по одной стене и 4 по другой, после чего он мог определить, что стены перпендикулярны друг другу, если между двумя этими отметками укладывалось 5 единиц (5 2= З 2+ 4 2). Так проблема измерения углов сводилась к проверке соотношения длин, то есть гораздо более простой операции.
ПРЕДШЕСТВЕННИКИ ТЕОРЕМЫ ПИФАГОРА
Египтяне и вавилоняне уже знали, что треугольник с соотношением сторон 3:4:5 прямоугольный, но, видимо, только греки заметили, что З 2+ 4 2= 5 2и, таким образом, первыми сформулировали теорему в ее общем виде. Тысячелетние китайская и индийская культуры тоже довольно рано обратили внимание на эту геометрическую особенность — проблема диагонали квадрата была известна в этих культурах, а вот в великих цивилизациях доколумбовой Америки или Африканского континента (за исключением Египта) она не ставилась. В любом случае, Пифагору или кому-то из его учеников принадлежит заслуга открытия того, что описанное выше соотношение справедливо для всех возможных прямоугольных треугольников.
Читать дальше













