Айзек Азимов - Числа - от арифметики до высшей математики

Вы можете спросить: что же это такое «бесконечно малая величина»? Конечно, самой малой величиной является ноль. Но малая величина может представлять собой

дробь. Скажем, 1/10 — это малая величина, 1/100 — еще меньше, 1/1000 — еще меньше, а 1/10000 — еще меньше. Не существует предела, до которого можно уменьшать величины. Но как бы вы ни увеличивали количество нулей в знаменателе, вы никогда не достигнете нуля. Таким образом, когда вы делите единицу или какое либо другое число на последовательность бесконечно возрастающих чисел, вы получаете последовательность бесконечно убывающих чисел. Когда делитель становится бесконечно большим числом, частное становится бесконечно малым.

Обратите внимание, что мы не можем делить числа на ноль. Эта операция в математике не рассматривается, и причина очень проста. Скажем, какое частное мы получим от деления 6 на 0? Другими словами, на какое число надо умножить 0, чтобы получить 6? Такого числа нет, значит, операция 6 : 0 невозможна. Любое число, умноженное на ноль, дает ноль. Это означает, что мы не можем ни одно число разделить на ноль.

Промежуток между двумя числами, скажем, между единицей и двойкой, можно разделить на любое количество долей, на миллион, триллион и так далее, бесконечно. То же самое можно проделать и с меньшим интервалом, скажем, с интервалом между ¼ и ½ или между 0,0000001 и 0,00000001.

Математики доказали, что все возможные дроби (то есть все рациональные числа) можно расположить таким образом, чтобы получить взаимно однозначную последовательность по отношению к последовательности целых чисел.

Для каждого целого числа будет существовать соответствующая дробь, и, наоборот, не может быть дроби без соответствующего целого числа. Таким образом, последовательности всех возможных дробей являются счетными последовательностями. 

Рассмотрим бесконечную последовательность дробей:

1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512...

Обратите внимание на то, что каждая следующая дробь равна половине предыдущей, поскольку знаменатель каждый раз удваивается. (Если взять любую дробь и разделить ее на 2, например 1/128 : 2, то это то же самое, что умножить ее на 1/2, то есть 1/128 : 2 = 1/128 × 1/2, а это значит, что знаменатель удваивается.)

Хотя дроби постоянно уменьшаются, эта последовательность также является бесконечной, ведь любую сколь угодно малую дробь из этой последовательности можно разделить на два и получить еще меньшую. Знаменатель дроби увеличивается бесконечно, но сама дробь никогда не достигнет нуля, поскольку для этого надо, чтобы знаменатель достиг бесконечности, а это невозможно.

А теперь давайте выясним, чему равна сумма этой бесконечной последовательности. С точки зрения простого здравого смысла может показаться, что сумма такой последовательности должна быть бесконечно большой величиной. Но мы уже знаем, насколько обманчив бывает так называемый «здравый смысл».

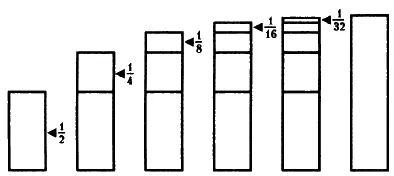
Сначала к 1/2 прибавляем 1/4, получаем 3/4, затем к 3/4 прибавляем 1/8, получаем 7/8, затем к 7/8 прибавляем 1/16, получаем 15/16, прибавляем 1/32, получаем 31/32 и так далее. Обратите внимание, что чем больше членов последовательности мы добавляем, тем ближе сумма последовательности приближается к 1. Когда мы складываем первые два члена ряда, до единицы остается 1/4, прибавляем следующий член, и до единицы остается 1/8, и так далее можно дойти до одной миллионной или до одной триллионной, но единица так никогда и не будет достигнута.

Математики так формулируют это положение: «Сумма бесконечной последовательности дробей 1/2, 1/4, 1/8… приближается к единице, которая является пределом суммы данной последовательности».

Это пример сходящейся последовательности, то есть последовательности, состоящей из бесконечного числа членов, сумма которых приближается к какому-либо конечному числу как к пределу.

Еще в Древней Греции математики обнаружили сходящиеся бесконечные последовательности, но они были столь поражены тем, что количество членов последовательности бесконечно, что даже не могли предположить, что сумма таких последовательностей может быть не бесконечной величиной. Греческий математик и философ Зенон поставил ряд задач, называемых парадоксами, которые, казалось бы, опровергают совершенно очевидные постулаты. Один из его парадоксов служил доказательством того, что движение в принципе невозможно. Эти парадоксы считались неразрешимыми на протяжении столетий, до тех пор, пока не выяснилась правда о сходящихся бесконечных последовательностях.