Вам понадобится довольно много времени, чтобы провести все необходимые операции деления и умножения, а используя метод логарифмов, если вы хорошо освоили правила работы с логарифмическими таблицами, можно решить этот пример очень быстро. Нужно будет несколько раз заглянуть в таблицы и провести несколько операций сложения и вычитания.
Далее, если по условиям вашей задачи вам достаточно получить ответ с определенным приближением — а в инженерных и научных расчетах именно это и требуется, — метод логарифмов дает дополнительное преимущество, поскольку он значительно сокращает время, необходимое для проведения вычислений.
Новые счеты
Ключ к сокращению времени вычислений мы найдем, если обратим внимание на характер логарифмической зависимости. Логарифм 1,0 равен 0,0000, логарифм 2,0 равен 0,3010, а логарифм 3,0 равен 0,4771. При увеличении числа от 1 до 2 величина логарифма увеличивается на 0,3010; при увеличении числа от 2 до 3 величина логарифма увеличивается на 0,1761. Логарифм 4,0 равен 0,6020, что означает увеличение на 0,1249. При увеличении числа от 9,0 до 10 логарифм увеличивается с 0,9542 до 1,0000, то есть только на 0,0458. При переходе от 19 к 20 логарифм увеличивается с 1,2788 до 1,3010, то есть только на 0,0222.
Теперь нанесем на один край линейки значения логарифмов, расположив их равномерно, а на другой край — соответствующие этим логарифмам числа (антилогарифмы).
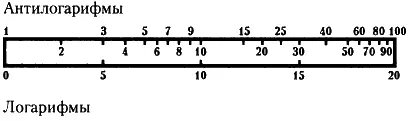
Подвижная логарифмическая шкала
Мы видим, что обычные числа располагаются все более часто с увеличением числа. Это отражает тот факт, что с увеличением числа скорость увеличения логарифма снижается.
Шкала, на которой числа расположены не равномерно, а соответственно величинам их логарифмов, называется логарифмической шкалой. Эта логарифмическая шкала стала основой для изобретения одного очень полезного инструмента для вычислений — логарифмической линейки, которая еще совсем недавно была необходима каждому инженеру, до тех пор, пока на смену ей не пришли калькуляторы и компьютеры.
Линейка устроена следующим образом. Если две обычные линейки, на которые нанесены логарифмические шкалы, двигать друг относительно друга, можно проводить операции сложения и вычитания, а поскольку шкалы на линейках логарифмические, это означает, что мы складываем или вычитаем логарифмы чисел, то есть перемножаем или делим сами числа.
Например, нам надо перемножить 2 и 3. Как показано на рисунке, устанавливаем подвижную часть линейки так, чтобы деление 1 на ней совпало с делением 3 на неподвижной части. Затем переводим взгляд на деление 2 на подвижной части и смотрим, против какого деления на неподвижной части оно установилось. Мы видим, что это 6. То есть логарифм 3 + логарифм 2 = логарифму 6, а 3 × 2 = 6.
На следующем рисунке показан эскиз настоящей логарифмической линейки с несколькими шкалами. Такая линейка позволяет быстро решать разнообразные задачи и производить сложные расчеты, точность которых зависит от размера делений шкал. Фактически такая линейка представляет собой компактную таблицу логарифмов.

Однако каждое новое достижение обычно сопровождается какими-то потерями. Точно так же дело обстоит и в случае с логарифмической линейкой. Линейка позволяет гораздо быстрее и удобнее производить вычисления, но есть и потери. При использовании таблиц логарифмов вам не надо самим определять положение десятичной запятой, оно уже указано в таблице. При расчетах на линейке вам придется определять положение десятичной запятой самостоятельно.
Для того чтобы определить положение десятичной запятой, необходимо грубо оценить ответ решаемой задачи. Например, мы вычисляем выражение, которое рассматривали ранее в этой главе:
(194,768 × 0,045 × 19,2 2) : (1,558 × 35,4).
Произведем округление чисел этого выражения и получим: (200 × 1/20 × 20 2) : : (1½ × 35), что равно (4000 : 50), или 80. Это означает, что ответ, который мы получим, точно решая приведенное выше выражение, будет находиться ближе к числу 80, нежели к 8 или 800. Таким образом, мы оценили положение десятичной запятой, или, другими словами, «порядок величины» будущего ответа.
Теперь, используя логарифмическую линейку, можно выполнить указанные действия. В результате мы получаем ответ 587, а поскольку мы знаем, что ответ должен находиться ближе к 80, чем к 8 или 800, то десятичную запятую можно смело ставить после второй значащей цифры слева, то есть получаем 58,7. Все расчеты при помощи логарифмической линейки, включая определение порядка величины, заняли у меня всего 35 секунд, хотя я считал не торопясь, чтобы не наделать ошибок.
Читать дальше













