Айзек Азимов - Числа - от арифметики до высшей математики

Например, рассмотрим пример умножения: 0,2 × 0,2.

Вы можете попробовать решить этот пример по аналогии со сложением: 2 + 2 = 4, также 2 × 2 = 4, тогда, поскольку 0,2 + 0,2 = 0,4. Возможно, и 0,2 × 0,2 = 0,4?

Нет, этого не может быть, и я сейчас докажу вам это.

Перейдем обратно к обыкновенным дробям, с которыми мы научились так хорошо обращаться. 0,2 = 2/10. Теперь перемножим дроби по старой методике: 2/10 × 2/10 = 4/100 (числитель умножаем на числитель, знаменатель на знаменатель). А 4/100 в десятичных дробях — это 0,04. Следовательно, 0,2 × 0,2 отнюдь не равно 0,4. 0,2 × 0,2 = = 0,04. Мы можем решить еще несколько примеров на умножение десятичных дробей, заменяя их на эквиваленты в обычных дробях. Например: 0,82 × 0,21 = 0,1772, а 0,82 × 2,1 = 1,772. (Это можно проверить следующим образом:

82/100 × 21/100 = 1722/10000, а 82/100 × 21/10 = 1722/1000.)

Теперь мы можем сформулировать общее правило: при перемножении десятичных дробей количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.

Так, при умножении 0,2 × 0,2 общее количество цифр справа от десятичной запятой в перемножаемых числах равно 2, и это означает, что 0,2 × 0,2 = 0,04 (ноль справа от десятичной запятой также является значащей цифрой).

Естественно, что если один из сомножителей является целым числом, то он не влияет на положение десятичной запятой. Положение десятичной запятой в произведении будет таким же, как и в том сомножителе, который является десятичной дробью.

То есть 0,2 × 2 = 0,4; 1,5 × 5 = 7,5; а 1,1 × 154 = 169,4.

Эти результаты соответствуют правилу умножения, и в любом случае количество цифр справа от десятичной запятой в ответе равно общему количеству цифр справа от десятичной запятой в перемножаемых числах.

Определить положение десятичной запятой в случае деления можно по аналогичной методике, действуя в обратном порядке. Но обычно при делении процедуру стараются упростить и приводят делитель или знаменатель (если деление проводят с помощью обычных дробей) к виду целого числа, не содержащего значащих чисел справа после запятой.

Предположим, нам надо 1,82 разделить на 0,2. Это выражение можно записать как 1,82/0,2. Не изменяя величины дроби, умножаем числитель и знаменатель на 10. Тогда 1,82 × 10 (в соответствии с правилом определения положения десятичного знака) равно 18,20, или 18,2, поскольку ноль, стоящий справа после последней значащей цифры, не изменяет величины числа и, следовательно, его можно опустить. Точно так же 0,2 × 10 = 2,0, или просто 2 (поскольку 2 плюс ноль десятых равно 2).

Следовательно, дробь можно записать как 18,2/2, и теперь знаменатель является целым числом, следовательно, при делении положение десятичного знака после запятой не меняется, так же как и в случае деления. Раз в числителе одна значащая цифра справа после запятой, то и результат должен иметь одну значащую цифру справа после запятой, то есть 18,2/2 =9,1.

Освоив деление десятичных дробей, мы сможем переводить обычные дроби в десятичные. Предположим, нам нужно найти десятичный эквивалент для 1/40. Мы можем представить эту дробь в виде 1,000/40, а затем произвести деление. Поскольку мы делим на целое число, то положение десятичной запятой не меняется. Проведем деление:

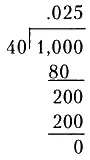
Таким образом, мы показали, что десятичный эквивалент 1/40 равен 0,025. Это можно проверить, переведя 0,025 в обычную дробь.

0,025 = 2/100 + 5/1000, или 20/1000 + 5/1000, или 25/1000, или если произвести деление, то получим 1/40, как мы и предполагали.

Вернемся к примерам умножения на 10. В предыдущих параграфах мы умножали 1,82 на 10 и получили 18,2. Обратите внимание, что умножение на 10 фактически просто сводится к тому, что мы перемещаем знак десятичной запятой на единицу вправо. Точно так же умножение на 100 сводится к перемещению знака десятичной запятой на две единицы вправо, а умножение на 1000 — соответственно на три единицы. В этом вы легко сможете убедиться самостоятельно.

Деление на 10 сводится к действию, обратному умножению, в данном случае к перемещению знака десятичной запятой на одну единицу влево, деление на 100 — на две единицы влево, а деление на 1000 — соответственно на три единицы влево.

Поскольку 1,82 : 10 согласно правилу обратных дробей равно также 1,82 × 0,1, что, в свою очередь, равно 0,182. Такой же ответ мы бы получили, если бы согласно правилу перемещения десятичной запятой передвинули запятую на один знак влево.