Айзек Азимов - Числа - от арифметики до высшей математики

Греческие математики занимались в основном геометрией и много времени проводили подсчитывая количество точек, расположенных на плоскости в форме различных геометрических фигур. Количество точек, которые составляют треугольник, называют треугольными числами.

Можно представить себе сверхмикроскопический треугольник, состоящий из одной точки. Три точки также образуют треугольник, у которого по две точки на каждой стороне. Шесть точек образуют уже больший треугольник, у которого по три точки на каждой стороне, а десять точек — треугольник, у которого по четыре точки на каждой стороне.

Можно записать треугольные числа в ряд: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 и так далее. Каждое следующее треугольное число образует треугольник, у которого на каждой стороне на одну точку больше. Ряд треугольных чисел можно продолжать бесконечно.

Обратите внимание, ряд треугольных чисел образует определенную зависимость. Первое число равно 1, следующее равно 3, то есть 1+2, затем идет 6, то есть 1 + 2 + 3, затем 10, то есть 1 + 2 + 3 + 4, затем 15, то есть 1 + 2 + 3 + 4 + 5, и так далее. Запомнив эту зависимость, вы сможете продолжать ряд треугольных чисел сколь угодно долго, не составляя треугольников и не пересчитывая точки. Определить, является ли данное число треугольным или нет, можно, представив его в виде ряда, подобного приведенному выше. Если число можно представить в виде суммы чисел, где каждое следующее число на единицу больше предыдущего, а первое число является единицей, то это число — треугольное.

Любая группа чисел, которая может быть представлена в виде последовательности, подчиняющейся какому-то правилу, образует ряд.

Числа, являющиеся количеством точек, из которых можно составить квадрат, тоже можно представить в виде ряда. Как и в прошлый раз, одну точку можно рассматривать как сверхмикроскопический четырехугольник. Четыре точки также образуют четырехугольник, у которого по две точки на каждой стороне. Девять точек образуют уже больший четырехугольник, у которого по три точки на каждой стороне, а шестнадцать точек — четырехугольник, у которого по четыре точки на каждой стороне.

Можно записать четырехугольные числа в ряд: 1, 9, 16, 25, 36, 49 и так далее. Каждое следующее четырехугольное число образует четырехугольник, у которого на каждой стороне на одну точку больше. Ряд четырехугольных чисел можно продолжать бесконечно.

Проанализировав числа, составляющие ряд четырехугольных чисел, мы увидим, что они тоже подчиняются определенной зависимости. Начнем с 1. Здесь нет вариантов, единица — это просто единица. Но уже 4 = 1 + 3, далее 9 = 1 + 3 + 5, 16=1+3 + 5 + 7 и так далее.

Таким образом, каждое число является суммой последовательных нечетных чисел, первое из которых единица.

Соотношение между числами треугольного и квадратного рядов показано на диаграмме.

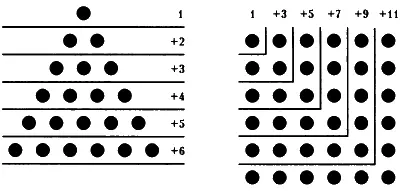
Соотношения в рядах треугольных и квадратных чисел

У греков был также ряд пентагональных чисел, которые представлены на рисунке. Этот ряд можно рассматривать как некий синтез треугольных и четырехугольных рядов. Если мы построим несколько пятиугольников таким же образом, как строили треугольники и четырехугольники, то получим числовой ряд вида 1, 5, 12, 22, 35, 51, 70 и так далее. Это ряд чисел, которые получают сложением чисел, отличающихся друг от друга на три. Первый член ряда — это единица. Второй — 5, то есть 1 + (1 + 3) = 1 + 4. Третий — 12, то есть 1 + 4 + (4 + 3) = 1 + 4 + 7, четвертый — 22, то есть 1 + 4 + 7 + 10, и так далее.

Греки изобрели и другие геометрические фигуры, моделирующие числовые ряды. Числа, составляющие такие последовательности, называются фигурными. Некоторые фигурные числа моделируются уже не плоскими фигурами, как треугольник и квадрат, а объемными, например кубами. Такие кубы трудно изобразить на рисунке, но если вы внимательно посмотрите на числовой ряд, вы сможете составить себе какое-то представление о кубической фигуре из точек. Серия кубических чисел — это ряд 1, 8, 27, 64, 125 и так далее.