Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

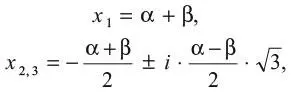
где i – мнимая единица, а

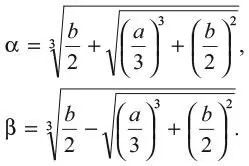
За неделю до состязания Тарталья был в отчаянии и боялся проиграть, но тут его посетило озарение: он понял, как решить остальные типы уравнений. И, конечно, он послал Фиоре только те уравнения, которые тот заведомо не мог решить.

Кардано прослышал об этом соревновании и понял, что оба соперника успели разработать методы для решения кубических уравнений. Мечтая вставить их в свою книгу, он обратился к Тарталье с просьбой поделиться с ним своими наработками. Тарталья, естественно, с неохотой пошел на это, ведь средства к его существованию зависели от них. Он долго колебался, но в итоге всё же его удалось уговорить. Кардано поклялся не публиковать новый метод. Тайна была нарушена в изданном Кардано труде «Великое искусство» («Ars magna»), и Тарталья имел полное право рассердиться. Он публично обвинил Кардано в плагиате.

Хотя Омар Хайям известен большинству из нас как поэт, он был также и выдающимся математиком.

Впрочем, Кардано никогда не мог похвастаться хорошей репутацией. Он был неисправимым игроком, готовым спустить любую сумму в карты, кости или даже шахматы. Так он умудрился проиграть все семейное состояние. С другой стороны, это был гений, талантливый врач, выдающийся математик и опытнейший самопиарщик, хотя его положительные качества часто бледнели на фоне излишней, подчас на грани оскорбления, откровенности. И гнев Тартальи, обвинявшего Кардано в обмане и воровстве, был вполне справедливым. То, что Кардано честно ссылался в своей книге на Тарталью, только усугубило положение. Тот понимал, что в памяти потомков останется автор книги, а не какое-то имя, мельком упомянутое в паре строк.

Но у Кардано было оправдание, и вполне весомое. Оно стоило того, чтобы нарушить обещание, данное Тарталье. Он включил в свою книгу новые открытия, сделанные им и его учеником Лодовико (Луиджи) Феррари, в том числе общее решение уравнения четвертой степени. Это было великое достижение, настоящий прорыв в науке. Конечно, Кардано не преминул включить его в свою книгу. Это считалось вполне законным, ведь открытие сделал его ученик. Однако метод Феррари сводит решение любого уравнения четвертой степени к соответствующему кубическому; следовательно, он основан на методе Тартальи. И Кардано не мог опубликовать работу Феррари, не включив в нее также и метод Тартальи.

А вскоре пришли новости, подсказавшие ему способ выйти из неловкого положения. У того самого Фиоре, что проиграл Тарталье в публичном соревновании, был ученик, Сципион дель Ферро. И до Кардано дошли слухи о том, что дель Ферро решил все три типа кубических уравнений, а не только то, с которым справился Фиоре, и что неопубликованные бумаги дель Ферро оказались в руках некоего Аннибала дель Наве. И вот Кардано с Феррари в 1543 г. отправляются в Болонью, чтобы повстречаться с дель Наве, посмотреть на его бумаги, и там – ясные как день – им открылись решения для всех трех типов уравнений. Итак, у Кардано появилась возможность спокойно заявить, что он опубликовал не метод Тартальи, а открытие дель Ферро.

Но Тарталья не смирился с поражением, хотя и не мог больше опровергать уверения Кардано о том, что приведенное им решение открыто дель Ферро. Тарталья опубликовал пространную и полную гнева диатрибу об этой несправедливости, и его вызвал на публичные дебаты Феррари, горевший желанием отстоять честь наставника. Он одержал грандиозную победу, а Тарталья так и не оправился от этого удара.

Итальянские математики эпохи Возрождения сделали немало важных алгебраических открытий, но их система записи всё еще была далека от совершенства. На развитие символов современной алгебры ушла не одна сотня лет.

Первым, кто предложил использовать символы для обозначения неизвестных величин, был Диофант Александрийский. Его «Арифметика», написанная примерно в 250 г., изначально содержала 13 книг, шесть из которых дошли до нас в виде позднейших копий. Труд посвящался решению алгебраических уравнений как с целыми, так и с рациональными числами – дробями вида p/ q, где p и q – целые числа. Нотация Диофанта сильно отличается от той, которой мы пользуемся сейчас. И хотя «Арифметика» – единственный из дошедших до нас трудов на эту тему, есть некоторые свидетельства того, что Диофант был частью более широкой традиции, а не просто отдельной фигурой.