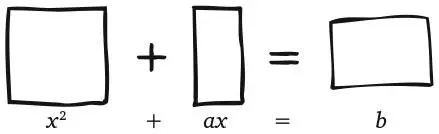
Здесь квадрат и первый прямоугольник имеют высоту x ; их ширина равна соответственно x и a . Меньший прямоугольник имеет площадь b . По вавилонскому рецепту мы легко делим первый прямоугольник на две половины:
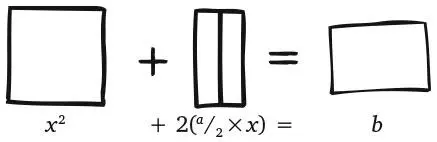
Два новых прямоугольника мы можем переместить и совместить с краями квадрата:
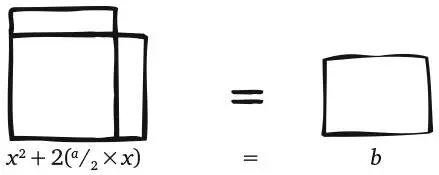
Получившаяся слева фигура так и просится быть дополненной до большого квадрата, с добавлением затененного квадрата.
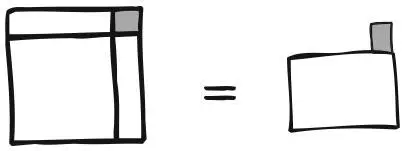
Чтобы уравнение оставалось верным, такой же квадрат должен быть добавлен и к левой фигуре. Но теперь мы определяем площадь последней как квадрат стороны ( x + a/ 2), и геометрическая схема эквивалентна алгебраическому выражению:
x 2+ 2( a/ 2× x ) + ( a/ 2) 2= b + ( a/ 2) 2.
Поскольку левая часть – квадрат суммы, мы можем переписать это так:
( x + a/ 2) 2= b + ( a/ 2) 2,
чтобы потом извлечь из него квадратный корень:
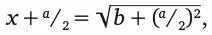
и наконец переписать в виде
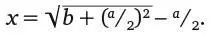
что в точности повторяет вавилонский вариант решения.
Ни на одной из табличек не найдено подтверждения гипотезе, что вавилоняне воспользовались этой геометрической схемой для получения своего алгоритма. Но такое объяснение не лишено смысла, так как косвенно подтверждается схемами, изображенными на других табличках.
Слово «алгебра» происходит от арабского «аль-джабр» – термина, использованного Мухаммадом ибн Мусой аль-Хорезми, ставшим известным в 820 г. В его работе «Краткая книга об исчислении аль-джабры и аль-мукабалы» изложены основные методы решения уравнений с неизвестными.
Аль-Хорезми использует слова, а не символы, но его методы узнаваемы и практически не отличаются от тех, которым нас учат сегодня. «Аль-джабр» означает «восполнение равных количеств к обеим сторонам уравнения». Так, мы начинаем:
x – 3 = 5
и выводим, что
x = 8.
Фактически мы делаем свой вывод, прибавляя по 3 к каждой из сторон. «Аль-мукабала» имеет два смысла. Вот его особый смысл: «вычитание равных количеств из обеих сторон уравнения», чем мы и занимаемся, переходя от
x + 3 = 5
к ответу
x = 2.
Но есть и более общий смысл: «восстановление», т. е. приведение подобных членов в обеих частях уравнения. Аль-Хорезми дает общие правила для шести видов уравнений, с помощью которых можно решить все линейные и квадратные уравнения. В его работах представлены идеи элементарной алгебры, но без использования символов.
Итак, вавилоняне умели решать квадратные уравнения, и их метод был по существу таким же, какому нас учат сегодня. Алгебраически самое сложное в нем – квадратный корень, и присутствует несколько стандартных арифметических действий (сложение, вычитание, умножение и деление). Ожидаемым следующим шагом становятся кубические уравнения, включающие неизвестное в кубе. Их мы пишем так:
аx 3+ bx 2+ cx + d = 0,
где x – неизвестное, а коэффициенты a, b и c – известные. Но до появления идеи отрицательных чисел математики классифицировали кубические уравнения по нескольким отдельным видам, так что, например, выражения x 3+ 3 x = 7 и x 3 – 3 x = 7 расценивались как совершенно разные, и для них существовали свои методы решения.
ЧИСЛА ФИБОНАЧЧИ
Третья часть «Книги абака» содержит задачу, автором которой, скорее всего, был сам Леонардо: «Некто поместил пару кроликов в место, со всех сторон окруженное стеною. Со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов; кролики никогда не умирают. Сколько пар кроликов будет через год?»
Эта каверзная задача приводит к любопытной последовательности чисел, получившей широкую известность:
Читать дальше
![Йэн Стюарт Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres] обложка книги](/books/419776/jen-styuart-ukrochenie-beskonechnosti-istoriya-matema-cover.webp)
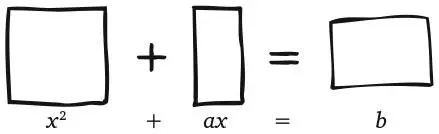
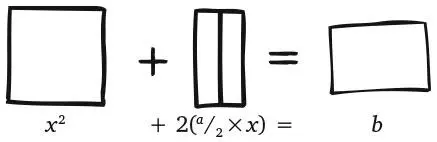
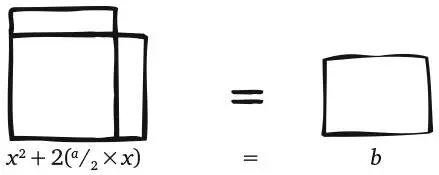

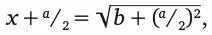
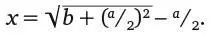





![Анна Одувалова - Высшая школа хаоса [litres]](/books/384215/anna-oduvalova-vysshaya-shkola-haosa-litres-thumb.webp)
![Ольга Пашнина - Богиня хаоса [litres]](/books/391340/olga-pashnina-boginya-haosa-litres-thumb.webp)
![Роджер Желязны - Владения Хаоса [litres]](/books/393502/rodzher-zhelyazny-vladeniya-haosa-litres-thumb.webp)
![Сара Бреннан - Дочь хаоса [litres]](/books/400527/sara-brennan-doch-haosa-litres-thumb.webp)
![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)

