Как вы думаете, количество целых чисел (и положительных, и отрицательных) больше количества натуральных? Будет ли их вдвое больше? Нет, потому что мы можем сопоставить эти два множества вот так:

Арифметика бесконечных кардинальных чисел тоже довольно странная. Например, мы только что увидели, что множества четных и нечетных натуральных чисел имеют кардинальное число א 0. Поскольку у них нет одинаковых элементов, кардинальное число их объединения – множества, полученного в результате их совмещения, – должно быть א 0+ א 0. Номы знаем, что представляет собой такое объединение: это натуральные числа с кардинальным числом א 0. Видимо, придется заключить:
א 0+ א 0= א 0.
Так мы и поступим. Но и здесь нет противоречий: мы не можем поделить א 0, чтобы получить 1 + 1 = 1, потому что א 0не является натуральным числом. Такое деление невозможно, поскольку не имеет смысла. Действительно, это равенство показывает, что деление на א 0не имеет смысла. И снова мы принимаем это как плату за прогресс.
Всё это очень хорошо, однако кому-то может показаться, что א 0не более чем новый забавный символ для старой доброй бесконечности и по сути ничего нового здесь не сказано. Разве это не тот случай, когда все бесконечные множества имеют кардинальное число א 0? Разве все бесконечности не равны?
Один из кандидатов на бесконечное кардинальное число, большее, чем א 0, – точнее, на бесконечное множество, для которого невозможно установить взаимно однозначное соответствие с множеством целых чисел, – это множество всех рациональных чисел, обычно обозначаемое Q. В конце концов, есть бесконечно много рациональных чисел в промежутке между двумя любыми последовательными целыми числами, и здесь уже не работает та хитрость, которая помогала нам с целыми числами.
Однако в 1873 г. Кантор доказал, что Q также имеет кардинальное число א 0. Взаимно однозначное соответствие основательно перемешивает числа, но никто и не говорил, что они должны располагаться согласно порядковым номерам. Кажется, всё выглядит замечательно: всякое бесконечное множество имеет кардинальное число א 0.
В том же году Кантор совершил важный прорыв. Он доказал, что последовательность 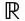 всех действительных чисел не имеет кардинального числа א 0. Неожиданную теорему об этом он опубликовал в 1874 г. Так что даже в неординарном понимании Кантора существует больше действительных чисел, чем целых. Одна бесконечность может быть больше другой.
всех действительных чисел не имеет кардинального числа א 0. Неожиданную теорему об этом он опубликовал в 1874 г. Так что даже в неординарном понимании Кантора существует больше действительных чисел, чем целых. Одна бесконечность может быть больше другой.
Насколько велика мощность действительных чисел? Кантор надеялся, что это будет א 1, следующее наибольшее кардинальное число после א 0. Но он не смог этого доказать и потому обозначил новое кардинальное число С, от первой буквы слова «континуум». Ожидаемое уравнение С = א 1было названо континуум-гипотезой. Математики сумели вывести соотношение между С и א 0только в 1960 г., когда Пол Коэн доказал, что ответ зависит от аксиом, которые вы выбираете для теории множеств. С одним разумным набором аксиом два кардинальных числа равны. Но с набором других, не менее обоснованных, аксиом они будут разными.
Обоснованность равенства С = א 1зависит от выбранных аксиом, но связанное с ним равенство от этого не зависит. Это равенство С = 2 א 0. Для любого кардинального числа A мы можем определить 2 Aкак кардинальное число множества (мощностью А ) всех его подмножеств. И мы можем очень легко доказать, что 2 Aвсегда больше A . Это значит, что не только некоторые бесконечности больше, чем другие, но и нет бесконечно большого кардинального числа.
Однако величайшей целью фундаментальной математики было все-таки не доказательство существования математических идей. Гораздо важнее было доказать, что математика логически последовательна. Ведь всем сегодня понятно: можно выстроить некоторую четкую последовательность безупречно правильных логических шагов, приводящую к абсурдному выводу. Может, вы соберетесь доказать, что 2 + 2 = 5 или 1 = 0, например. Или что 6 – простое число, или что π = 3.
Ведь может показаться, что одно незначительное противоречие будет иметь ограниченные последствия. В быту люди вообще спокойно воспринимают такие противоречия, заявляя в один момент, что глобальное потепление уничтожает планету, а в другой – что авиакомпании-лоукостеры – гениальное изобретение. Но для математики последствия не могут быть ограниченными, и вы не избежите логических противоречий, просто закрыв на них глаза. В математике, как только что-то доказано, вы можете использовать это для других доказательств. Доказательство того, что 0 = 1, повлечет еще больше неприятностей. Например, утверждение, будто все числа равны. Если x – любое число, то сначала умножим обе части равенства 0 = 1 на х . Тогда 0 = x . И если y – любое другое число, то 0 = y . Значит, x = y .
Читать дальше
![Йэн Стюарт Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres] обложка книги](/books/419776/jen-styuart-ukrochenie-beskonechnosti-istoriya-matema-cover.webp)

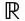 всех действительных чисел не имеет кардинального числа א 0. Неожиданную теорему об этом он опубликовал в 1874 г. Так что даже в неординарном понимании Кантора существует больше действительных чисел, чем целых. Одна бесконечность может быть больше другой.
всех действительных чисел не имеет кардинального числа א 0. Неожиданную теорему об этом он опубликовал в 1874 г. Так что даже в неординарном понимании Кантора существует больше действительных чисел, чем целых. Одна бесконечность может быть больше другой.




![Анна Одувалова - Высшая школа хаоса [litres]](/books/384215/anna-oduvalova-vysshaya-shkola-haosa-litres-thumb.webp)
![Ольга Пашнина - Богиня хаоса [litres]](/books/391340/olga-pashnina-boginya-haosa-litres-thumb.webp)
![Роджер Желязны - Владения Хаоса [litres]](/books/393502/rodzher-zhelyazny-vladeniya-haosa-litres-thumb.webp)
![Сара Бреннан - Дочь хаоса [litres]](/books/400527/sara-brennan-doch-haosa-litres-thumb.webp)
![Йэн Стюарт - Математика космоса [Как современная наука расшифровывает Вселенную]](/books/429584/jen-styuart-matematika-kosmosa-kak-sovremennaya-nau-thumb.webp)

