Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

В 1840-е гг. на этот текст, вернувшийся к тому моменту обратно в Константинополь и находившийся в греческой православной библиотеке, наткнулся библеист Константин фон Тишендорф. Он вынул из книги один лист и поместил его в библиотеку Кембриджского университета. В 1899 г. Афанасий Пападопуло-Керамевс, составляя каталог библиотечных рукописей, частично перевел этот лист. Гейберг понял, что текст принадлежит Архимеду, и проследил судьбу книжной страницы обратно до Константинополя, где ему разрешили сфотографировать весь документ. Затем он переписал текст и издал результаты своей работы между 1910 и 1915 гг., а Томас Хит перевел текст на английский язык. После сложной цепочки событий, включая продажу на аукционе, осложненную судебной тяжбой по поводу права собственности на документ, рукопись была продана анонимному американцу за $2 млн. Новый владелец предоставил ее для исследований, так что затертый текст восстановлен с применением различных цифровых технологий обработки изображений.

Чтобы доказывать теорему методом исчерпывания, нужно заранее знать ответ, и ученые долгое время гадали, как Архимед сумел угадать правила определения площади поверхности и объема сферы. Трактат «О методе» поясняет:

Действительно, кое-что из того, что ранее было мною усмотрено при помощи механики, позднее было также доказано и геометрически, так как рассмотрение при помощи этого метода еще не является доказательством; однако получить при помощи этого метода некоторое предварительное представление об исследуемом, а затем найти и само доказательство гораздо удобнее, чем производить изыскания, ничего не зная [2] Архимед. Сочинения. – М.: Физматлит, 1962. .

Архимед мысленно уравновешивает шар, цилиндр и конус на весах, а затем нарезает их бесконечно тонкими ломтиками, которые перераспределяет таким образом, чтобы сохранить баланс. Затем он применяет закон рычага, чтобы соотнести три объема между собой (объемы цилиндра и конуса был уже известны), и выводит требуемые величины. Существуют предположения, что именно Архимед первым использовал настоящие бесконечно малые величины в математике. Возможно, мы усматриваем слишком много в этом не самом вразумительном документе, но ясно, что трактат «О методе» предвосхищает некоторые идеи дифференциального исчисления.

Другие труды Архимеда наглядно показывают, насколько разнообразными были его интересы. Трактат «О спиралях» доказывает некоторые фундаментальные утверждения о длинах и площадях, связанных с Архимедовой спиралью – кривой, которую описывает точка, движущаяся с постоянной скоростью вдоль прямой линии, вращающейся с постоянной скоростью. Трактат «О коноидах и сфероидах» исследует объемы сегментов объемных тел, образованных вращением конических сечений вокруг некоторой оси.

Трактат «О плавающих телах» – первая в истории работа по гидростатике и равновесным позициям плавающих объектов. В него входит и закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной этим телом. Этот принцип является темой знаменитого исторического анекдота, в котором Архимеда просят придумать метод, при помощи которого можно определить, действительно ли обетная корона, изготовленная для царя Гиерона, сделана из золота. Идея решения осеняет Архимеда внезапно, когда он принимает ванну, и он приходит в такой восторг, что выскакивает на улицу, позабыв одеться, и несется по городу в чем мать родила с криком «Эврика!» («Нашел!»). Не забывайте, что появление нагого человека в публичном месте в Древней Греции не рассматривалось как скандальное событие. Кульминацией книги является условие устойчивого плавания параболоида – предтеча фундаментальных идей теории кораблестроения, связанных с остойчивостью и переворачиванием судов.

В «Измерении круга» метод исчерпывания применяется для доказательства того, что площадь круга равна длине половины радиуса, умноженной на длину окружности, – π r 2в современных терминах. Чтобы доказать это, Архимед вписывает в окружность и описывает вокруг нее правильные многоугольники с 6, 12, 24, 48 и 96 сторонами. Рассматривая девяностошестиугольник, он доказывает результат, эквивалентный, по существу, оценке величины π: он попадал в промежуток между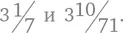

«Исчисление песчинок» адресовано Гелону II, тирану Сиракуз и сыну Гиерона II. Это подкрепляет предположение о том, что Архимед был в родстве с царской семьей. Он так объясняет свою цель: