Агниджо Банерджи - Эта странная математика. На краю бесконечности и за ним

Есть в математике и другие вещи и явления, которые на первый взгляд не имеют ничего общего с машинами Тьюринга, но на поверку оказываются их эквивалентами (эмулирующими их). Один из примеров – игра “Жизнь”, придуманная английским математиком Джоном Конвеем. Идея игры пришла ему в голову, когда он заинтересовался проблемой, которую в 1940-х годах исследовал венгерско-американский математик и один из основоположников компьютерной науки Джон фон Нейман: возможно ли выдумать гипотетическую машину, способную производить точные копии самой себя? Фон Нейман доказал, что это возможно, создав математическую модель такой машины, где использовались разбитая на прямоугольные клетки область и набор очень сложных правил. Конвей задался вопросом, нельзя ли доказать то же более простым способом, – и придумал игру “Жизнь”. В игре Конвея используется (теоретически) бесконечное поле, разбитое на квадратные клетки, каждая из которых может быть окрашена либо в черный, либо в белый цвет. Игра начинается с произвольного узора из черных клеток и развивается по двум правилам:

1. Черная клетка остается черной, если ровно 2 или 3 из восьми соседних клеток тоже черные.

2. Белая клетка превращается в черную, если ровно 3 соседние клетки – черные.

Вот и все. И хотя освоить игру “Жизнь” может даже ребенок, она обладает всеми теми же возможностями, что и универсальная машина Тьюринга – а стало быть, что и любой когда-либо созданный в истории человечества компьютер. Впервые удивительная игра Конвея была представлена широкой аудитории в колонке Мартина Гарднера “Математические игры” в октябрьском выпуске журнала Scientific American за 1970 год. Гарднер познакомил своих читателей с основными фигурами в игре: “блоком” – квадратом размером 2 × 2 клетки, который по правилам игры никогда не изменяется, и “мигалкой” – прямоугольником размером 1 × 3 клетки, ориентация которого чередуется между горизонтальной и вертикальной, а центр остается неподвижным. “Планер” представляет собой фигуру из пяти клеток, передвигающуюся по диагонали на одну клетку за каждые четыре хода.

Поначалу Конвей думал, что, как бы ни располагались клетки в начале игры, их бесконечное “размножение” невозможно – любая конфигурация в конце концов стабилизируется, превратится в осциллятор или просто исчезнет, “умрет”. В той статье Гарднера 1970 года объявлялось, что Конвей предлагает премию в 50 долларов первому, кто докажет или опровергнет эту гипотезу. Не прошло и нескольких недель, как приз получила группа из Массачусетского технологического института под руководством математика и программиста Билла Госпера, одного из основателей сообщества хакеров. Так называемое “ружье Госпера” циклически “выстреливает” нескончаемую череду планеров со скоростью одна штука за тридцать поколений. Помимо того, что это увлекательное зрелище, “ружье Госпера” представляет интерес и с точки зрения теории: оно играет важнейшую роль в построении компьютеров на основе игры “Жизнь”, поскольку испускаемые им планеры можно принять за аналог потока электронов в компьютере. В реальной жизни, правда, эти потоки надо как-то контролировать, чтобы компьютер мог выполнять свое предназначение – вычислять. Как раз эту функцию выполняет логический вентиль.

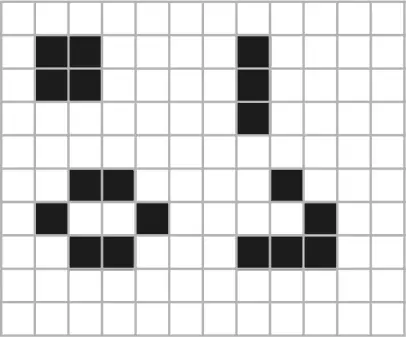
Четыре распространенных конфигурации в игре “Жизнь”. Слева : “блок” ( вверху ) и “улей” ( внизу ). Обе эти фигуры – “натюрморты”, то есть они не меняются в ходе игры. Фигура справа вверху – “мигалка”, простейший из осцилляторов, которые после нескольких поколений возвращаются в исходную конфигурацию. В случае с “мигалкой” вертикальная ориентация чередуется с горизонтальной. Фигура справа внизу – “планер”.

“Планер”, через четыре поколения передвигающийся на одну клетку по диагонали.

Логический вентиль – это электронный компонент, преобразующий один или более входных сигналов в выходной сигнал. В принципе, компьютер можно создать, используя всего один тип логического вентиля, но, если взять три, задача существенно упростится. Речь о вентилях НЕ, И и ИЛИ. Вентиль НЕ выдает на выходе сигнал высокого уровня тогда и только тогда, когда получает на входе сигнал низкого уровня. Вентиль И выдает на выходе сигнал высокого уровня тогда и только тогда, когда оба входных сигнала – высокого уровня. Наконец, вентиль ИЛИ выдает сигнал высокого уровня тогда и только тогда, когда хотя бы один из входных сигналов – высокого уровня. Вентили можно объединять в схемы, способные и обрабатывать, и хранить данные.