Gustavo Pineiro - У интуиции есть своя логика. Гёдель. Теоремы о неполноте.

Г итлер приветствует жителей Вены в связи с присоединением Австрии к нацистской Германии, март 1938 года.

Адель Поркерт и Курт Гёдель в день свадьбы, сентябрь 1938 года.

Немецкий математик Давид Гильберт в 1930-е годы. Созданная им программа стремилась поставить математику на прочные логические основания.

Прежде чем последовать за Гёделем в Принстон, вернемся в сентябрь 1930 года и восстановим образ юноши, который скромно поднял руку на конгрессе в Кёнигсберге, чтобы провозгласить первую теорему о неполноте.

Естественный вопрос, который мы еще не формулировали, состоит в следующем: после десяти лет разработки своей программы, размышлений и трудов сдался ли Гильберт без борьбы? Не пытался ли он оспорить рассуждения Гёделя? Правда состоит в том, что доказательство Гёделя было принято мгновенно и единодушно всеми, включая Гильберта, поскольку Гёдель не только очень хорошо продумал доказательство, но и был очень осторожен в способе его представления.

Как мы уже сказали, в программе Гильберта принимались только те доказательства, которые можно проверить алгоритмически, и к сентябрю 1930 года это ограничение принимали все математики, включая интуиционистов, которые, по словам Аренда Гейтинга, "примут с распростертыми объятиями" бесконечность, если только доказательства будут соответствовать этому критерию.

И так же, как Гильберт в свое время внес предложение с расчетом на то, чтобы убедить интуиционистов, Гёдель изложил доказательство первой теоремы о неполноте так, чтобы было очевидно, что ее правильность можно проверить алгоритмически и что она удовлетворяет условиям программы Гильберта. Даже Гильберт не смог выразить сомнений по этому поводу.

Как хорошо известно, прогресс математики в отношении каждый раз все большей точности привел к [...] тому, что рассуждения можно осуществить на основе небольших механических правил.

Курт Гёдель, введение к "О формально неразрешимых предложениях... " (1931)

Как Гёдель сделал очевидным, что доказательство его теоремы проверяется компьютером? Он прибегнул к "семантикосинтаксическому дуализму".

В математической логике понятие, связанное с последовательностью символов, считается синтаксическим, если оно зависит только от символов, образующих эту последовательность, при этом неважно его значение, если оно вообще существует.

Например, если мы утверждаем, что последовательность букв Кипа mbwa nyekundu образована 18 символами (считая пробелы), мы говорим о синтаксическом понятии. Действительно, нашу правоту легко проверить с помощью простого подсчета символов, и нас не интересует, есть ли в этом ряду букв какой- то смысл. Другие примеры синтаксических понятий: "первая буква — /С" или "здесь нет буквы А".

Наоборот, если понятие семантическое, оно зависит от значения, которое передает последовательность. Например, если мы говорим, что Кипа mbwa nyekundu истинно, то ясно, что мы говорим о семантическом понятии, потому что не можем сказать, является оно "истинным" или "ложным", если предварительно не узнаем, какое значение заложено в этой последовательности букв (если оно там есть).

На самом деле смысл в высказывании есть: Кипа mbwa nyekundu на суахили означает "бывают красные собаки" (см. рисунок). Теперь мы можем задаться вопросом, истинно предложение или ложно, но все равно ответ дать непросто. Ведь что такое красная собака? Она должна была родиться со шкурой такого цвета или ее могли покрасить позже? Уж не говоря о том, что люди воспринимают цвета по-разному. Целью всех этих рассуждений является пояснение: синтаксические аспекты языка прозрачны, а вот семантические — связаны с путаницей и парадоксами. В соответствии с этой идеей основная предпосылка программы Гильберта состояла в требовании того, чтобы справедливость семантических аспектов математики контролировалась синтаксическими методами. Синтаксис, ясный и не вызывающий сомнений, должен был ограничивать семантику, грозящую парадоксами.

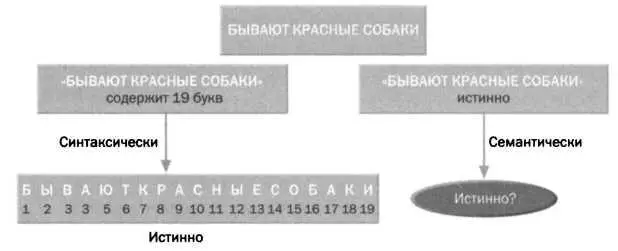
Свойство, относящееся к предложению, называют синтаксическим, если оно зависит только от самих символов, независимо от их значения (например, количество букв в предложении).