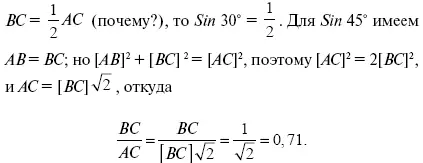Яков Перельман - Живой учебник геометрии

Р е ш е н и е (черт. 233). Если сторона 12-угольника АВ , то, соединив концы ее с центром О , получаем равнобедренный треугольник, угол при вершине которого 360°/12=30°.

Проведя OD перпендикулярно к AB , имеем прямоугольный треугольник AOD , в котором катет AD = ?АВ (почему?).

Далее:

AD/OD=AD/80 = tg15°=0,26

откуда:

AD = 0,26 80 = 21,

АВ = 2 AD = 42.

Итак, искомая сторона 12-угольника 42 см.

Рассмотрим задачу:

На плоскости AB (черт. 234), наклоненной под углом 35°, лежит тело весом 20 кг. С какою силою нужно тянуть тело вдоль плоскости AB , чтобы удержать его от скольжения вниз (трения в расчет не принимать)?

Р е ш е н и е. Очевидно, нужно тянуть с силою, не меньшею той, с какою тело увлекается своим весом. В механике установлено правило, что тело, лежащее на наклонной плоскости, увлекается вдоль нее с силою, составляющей такую долю веса тела, какую высота ВС наклонной плоскости составляет от ее длины AB. Это отношение зависит только от величины угла A , но не зависит от того, в какой точке наклонной плоскости (черт. 235) мы станем мерить ее высоту и длину: отношение ВС : AB = отношению DE: AD = отношению MN: AM и т. п. (почему?). Это отношение противолежащего катета к гипотенузе в треугольнике, отсекаемом от острого угла перпендикуляром к одной из его сторон, называется с и н у с о м этого угла и обозначается знаком sin :

SinA = BC/AB

Каждый угол имеет определенный синус, величина которого всегда может быть вычислена (по способу, излагаемому в подробных учебниках математики) или, менее точно, найдена из чертежа.

Если станем изменять величину угла от 0° до 90° и следить, как изменяется при этом величина синуса, то заметим следующее.

Когда угол близок к 0°, то и синус его близок к нулю: Sin 0° = 0. С увеличением угла sin его возрастает, но никогда не превышает 1-цы (почему?). При 90° величина его равна 1, потому что при этом катете сливается с гипотенузой; следовательно, sin 90° = 1.

Синус некоторых углов вычисляется очень просто. Например, синус 30° (черт. 230) равен

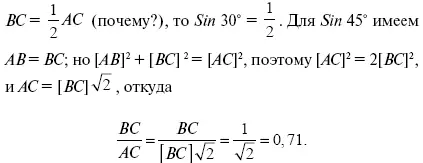
Вычисление sin 60 ° проделайте сами.

Отношение п р и л е ж а щ е г о к а т е т а к гипотенузе называется к о с и н у с о м угла А и обозначается cos. Напр. (черт. 229 и 230) cos 60° = BC: AC= 0,5; cos 45° = sin 45° = 0,71.

Между синусом и косинусом острого угла и его дополнительного существует та же зависимость, что и между tg и cot g: с и н у с о с т р о г о у г л а р а в е н к о с и н у с у д о п о л н и т е л ь н о г о у г л а (выведите это правило).

Поэтому таблицу синусов и косинусов можно свести в одну, как и сделано в таблице, напечатанной в конце книги.

Нахождение в таблице sin и cos данных углов, а также обратное нахождение углов, отвечающих данным синусу или косинусу, выполняется так же, как и в случае tg и cotg. Например, sin 12° = cos 78° = 0,21; sin 37°30 = 52°30 = = 0,61; cos 38°40 = sin 51°20 = 0,79; cos 14° = sin 76° = 0,24. Угол, sin которого 0,15, равен 8°30 , и т. п.

Возвращаясь к задаче о теле, скользящем по наклонной плоскости, находим sin 35° = 0,57; следовательно, для удержания груза необходима сила в 20 ? 0,57 = 11 кг.

Применения

109. Гипотенуза – 47 см, катет– 19 см. Найти величину противолежащего угла.

Р е ш е н и е. Синус искомого угла 19/47 = 0,42; отсюда угол = 25°.

110. Боковая сторона равнобедренного треугольника -

96 см; угол при вершине – 67°. Найти основание.

Р е ш е н и е. Синус половины угла при вершине, т. е. sin 33°30’ равен половине основания, деленной на длину боковой стороны; отсюда половина основания равна боковой стороне, умноженной на sin 33°30’ = 96 0,55 = 53.

111. Одна сторона треугольника 57 см, а другая – 81 см.

Угол между ними 47°. Найти длину перпендикуляра, проведенного к большей из данных сторон через противоположную вершину.

Р е ш е н и е. Пусть в треугольнике АВС (черт. 232) сторона АВ = 57, АС = 81, а угол А = 47°. Проведем ВD под прямым углом к АС , видим, что BD/ AB = BD/57 = sin 47°

откуда BD = 57 ? 0,68 = 39 см.

Если бы данный угол был тупой, например в 125° (черт. 236), то длину ВD мы узнали бы из отношения