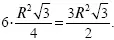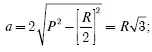Яков Перельман - Живой учебник геометрии

Р е ш е н и е. Так как сторона правильного вписанного шестиугольника = радиусу описанного круга, то искомый диаметр круга = 14 см.

98. На черт. 223 изображен контур стропил так наз. мансардной крыши, Он начерчен так: полуокружность разделена на 4 равные части и точки деления соединены прямыми.

Определите длины СЕ u FD, если пролет AB = 10 м.

Р е ш е н и е. Дуга СЕ составляет 1/4 окружности; значит, хорда СЕ равна стороне вписанного квадрата. Так как радиус окружности известен (5 м), то длина СЕ =5 ?2 = 7 м. Стрелка DFопределяется как разность GD– GF= 5 – 3,5 = 1,5 м.

99. В круге радиуса 100 см проведены две хорды, дуги которых 90° и 120°. На сколько сумма их длин отличается от длины полуокружности? Какой отсюда вытекает способ приближенного распрямления окружности?

Р е ш е н и е. Хорда дуги в 90° равна стороне вписанного квадрата = 100? ?2 = 141. Хорда дуги в 120° равна стороне вписанного равностороннего треугольника = 100 ??3 = 173.

Сумма их 141 + 173 = 314. Длина полуокружности радиуса 100 (при ? = 3,14) равна также 314. Значит, сумма этих хорд равна длине полуокружности до 4-й значащей цифры. Выпрямляя окружность, можно отложить на прямой две стороны вписанного квадрата и две стороны вписанного равностороннего треугольника.

100. Вычислить площадь заштрихованных частей фигуры черт. 224, если радиус круга = R.

Р е ш е н и е. Легко видеть, что каждая из трех заштрихованных частей представляет собою два сегмента, отсекаемых стороною правильного вписанного шестиугольника. Все три заштрихованные части равны по площади шести таким сегментам, т. е. разности между площадью круга и площадью вписанного в него правильного шестиугольника. Последняя площадь равна 6-кратной площади равностороннего треугольника со стороною R , т. е.

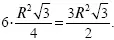
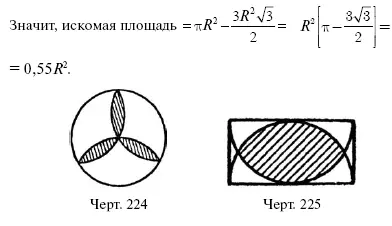
101. Какую долю площади наружного прямоугольника (черт. 225) составляет его заштрихованный участок.

Р е ш е н и е. Рассматривая чертеж, можно усмотреть, что заштрихованный участок представляет собою два сегмента, отсекаемые стороною такого вписанного многоугольника, апофема которого ?= радиуса. Обозначив радиус через R , имеем для длины этой стороны a выражение

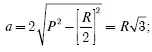
очевидно, хорда есть сторона вписанного равностороннего треугольника. Площадь равностороннего треугольника со стороною а равна площадь круга радиуса R равна ? R 2; отсюда площадь заштрихованной части

Так как площадь наружного прямоугольника = 2 R 2, то искомое отношение = 0,61.

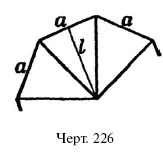
Пусть у нас имеется правильный многоугольник о n сторонах. Чтобы определить его площадь, соединим его центр со всеми вершинами: многоугольник разделится на n равных треугольников (почему они равны?). Если сторона многоугольника а , а апофема, т. е. высота каждого треугольника – l , то площадь одного треугольника равна ? аl , а всех треугольников в n раз больше:

n?? аl = ? nal .

Это и есть формула для вычисления площади правильного многоугольника. Ее можно несколько видоизменить, если принять во внимание, что na – есть сумма сторон многоугольника, т. е. его периметр P . Поэтому полученную сейчас формулу можно представить в таком виде:

S= ?Pl.

Словесно правило вычисления площади правильного многоугольника можно высказать так:

п л о щ а д ь п р а в и л ь н о г о м н о г о у г о л ь н и к а р а в н а п о л о в и н е п р о и з в е д е н и я е г о п е р и м е т р а н а а п о ф е м у.

Применения

102. Какова должна быть сторона шестиугольной шашки торцовой мостовой, чтобы на 1 кв. метр шло 30 шашек?

Р е ш е н и е. Если искомая сторона шашки x , то площадь

основания = 6 x 1/2 апофемы. Апофема =x?3/2 следовательно площадь = 6x?x?3/4=3x2?3/4 30 таких площадей равны 1 кв. м =10 000 кв. см. Имеем уравнение

30 ? 3x2?3/4 =10 000, откуда х = около 27 см.

103. Чему равна площадь сегмента, отсекаемого хордой равной радиусу R круга.