Яков Перельман - Живой учебник геометрии

D/ AB = BD/57 = Sin BAD = Sin [ 180 ° – 125 °] = Sin 55 ° = 0,57, откуда BD = 32 см.

112. По данным предыдущей задачи вычислить длину третьей стороны (черт. 232).

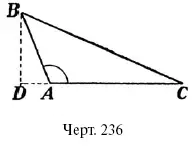
Р е ш е н и е. Из треугольника АВD находим длину отрезка AD (как?); вычтя эту длину из АС, узнаем DС; вычислив кроме того, длину ВD, находим сторону ВС из треугольника ВDC по правилу Пифагора.

Произведите это вычисление. Рассмотрите случай, когда угол = 125°, как на черт. 236.

113. Одна сторона треугольника 95 см; два угла его 35° и 61°. Найти остальные стороны.

Р е ш е н и е. Пусть в треугольнике АВС (черт. 232) сторона ВС = 95 см, угол A = 61°, угол С = 35°. Проведя через В перпендикуляр BD, вычисляем его длину из треугольника BDC (как?), а зная BD находим из треугольника ABD длину АВ (как?). Для вычисления длины АС находим отрезки AD и ВС (как?) и складываем их.

Другой ответ получим, если примем, что сторона в 95 см лежит против угла в 35°.

114. Радиус круга 120 см. Найти длину хорды, «стягивающей» дугу в 48°. (О хорде говорят, что она «стягивает» ту дугу, которая расположена между ее концами).

Р е ш е н и е. Если (черт. 219) дуга АпВ = 48°, то центральный угол О = 48°. Нахождение длины АВ сводится к вычислению основания равнобедренного треугольника по боковой стороне [ ОА ] и углу при вершине; задача эта уже рассмотрена нами ранее (см. задачу 110).

115. Вычислить сторону правильного семиугольника, вписанного в круг радиуса 30 см.

Р е ш е н и е. Если АВ (черт. 219) есть сторона правильного вписанного семиугольника, то угол О =360°/7= 51°4?

Следовательно, задача сводится к предыдущей.

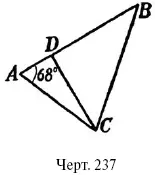
116. Одна сторона треугольника равна 24 см, другая – 31 см. Угол между ними – 68°. Найти площадь этого треугольника.

Р е ш е н и е. Проведем в треугольнике ABC высоту CD к стороне АВ , длина которой 24 см. Высота эта CD = AC sin A = 31 sin 68°. Следовательно, площадь ABC равна ??24?31 ? sin 68°

Нетрудно убедиться, что вообще, когда известный угол меньше прямого, то п л о щ а д ь т р е у г о л ь н и к а р а в н а п о л у п р о и з в е д е н и ю д в у х е г о с т о р о н н а с и н у с у г л а м е ж д у н и м и. Пользуясь только сообщенными здесь знаниями нельзя решить, все задачи, могущие возникнуть на практике. Подробное ознакомление с отраслью математики, которая называется тригонометрией, открывает гораздо более широкие возможности. Однако, и помощью тех начальных сведений из тригонометрии, которые изложены в этой главе, удается все же успешно разрешать многие практические задачи.

Повторительные вопросы

Что называется тангенсом? Котангенсам? Поясните ваш ответ чертежом. – Как они обозначаются? Укажите доступный вам приближенный способ определения тангенса и котангенса для любого острого угла. – Определите по этому способу tg и cotg нескольких углов и сравните ваши результаты с данными таблицы. – Как изменяется tg при изменении величины угла от 0° до 90°? – Чему равен cotg 0°? Чему равен tg 30°? tg 45°? tg 60°? Чему равны cotg этих углов? Какая вообще зависимость между tg и cotg одного и того же угла? – Какие углы называются дополнительными? – Какая зависимость между tg острого угла и cotg дополнительного угла? Найдите по таблице tg 26°, tg 38°30’; tg 79°? cotg 83°? – Найдите угол, tg которого равен 0,08? 1,35? cotg которого = 2,3? 0,59? Приведите примеры задач, разрешаемых помощью tg или cotg .

Что называется синусом? h осину сом? Как они обозначаются? Определите с помощью чертежа sin и cos нескольких углов и проверьте ваш результат по таблице. Как изменяется sin и как изменяется cos при изменении величины угла от 0° до 90°. Чему равен sin 45°? cos 45°? sin 30°? cos 30°? sin 60°? cos 60°? Какая зависимость между синусом острого угла и косинусом дополнительного угла? Найдите по таблице: sin 23°, sin 65°, cos 18°, cos 71°. Найдите углы, sin которых: 0,81; 0,13; 0,06; cos которых – 0,76; 0,18; 0,09. Приведите примени задач, разрешаемых с помощью sin или cos .

В §§ 34–37 и 40 мы познакомились с правилами вычисления поверхности и объема призм и цилиндра. Теперь рассмотрим несколько других тел, часто встречающихся на практике: так наз. «пирамиды», «конусы» и «шары».