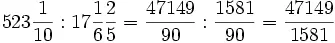
Въ XVI ст. по Р. X. на сцену вышло новое правило дѣленія дробей: надо дѣлимое помножить на обращеннаго дѣлителя. Примѣръ: ¾ : ⅔. Для рѣшенія его множимъ ¾ на 3/ 2, получимъ 9/ 8, это и будетъ вѣрнымъ отвѣтомъ. Въ объясненіе этого правила, равно какъ и всѣхъ другихъ, авторы учебниковъ входить не любили. Они только ограничивались тѣмъ, что приводили самое правило и потомъ нѣсколько примѣровъ съ рѣшеніемъ. Ученики же запоминали правило и практиковались въ примѣненіи его къ вычисленіямъ.
Знакомъ дѣленія до XVIII ст. являлись, обыкновенно, двѣ перекрещивающихся черты, которыя шли отъ числителя первой дроби къ знаменателю второй и отъ знаменателя первой къ числителю второй. Только съ развитіемъ алгебры, когда потребовался общій знакъ дѣленія и для цѣлыхъ чиселъ и для дробей, стали обозначать это дѣйствіе такъ же въ дробяхъ, какъ и въ цѣдыхъ числахъ, т.-е. двумя точками.
Приведемъ еще неболыпой интересный отрывокъ, который хорошо показываетъ, къ какимъ хитростямъ нужно было прибѣгать средневѣковымъ ученымъ, когда имъ давался трудный примѣръ съ дробями. Въ Зальцбургскомъ (Австрія) сборникѣ, отноеящемся къ XVII вѣку [1], надо было вычислить земной радіусъ по окружности земли. Извѣстно, что окружность въ 3 1/ 7раза больше своего радіуса, и поэтому, чтобы получить радіусъ земли, достаточно ея окружность раздѣлить на 22/ 7. Принимая окружность за 252000, составитель находитъ 7/ 22этого числа, т.-е. умноженіемъ на 7/ 22замѣняетъ дѣленіе на 22/ 7. Умноженіе же онъ ведетъ такъ. Сперва вычисляетъ 1/ 22всего числа, получится 11454½, затѣмъ вычитаетъ эту величину изъ 252000, будетъ 240544½ 21/ 22. Треть этого числа и составитъ искомый отвѣтъ, т.-е. земной радіусъ, такъ какъ 21/ 22: 3 = 7/ 22.
Древніе халдеи, образованность которыхъ исходитъ изъ глубины вѣковъ и позволяетъ прослѣдить свои пути далѣе, чѣмъ на 1000 лѣтъ до Р. X., издавна любили считать по копамъ, т.-е. группами по 60. Почему они остановились именно на этомъ числѣ,—теперь рѣшить, конечно, нелегко, но выборъ этотъ надо считать чрезвычайно удачнымъ, такъ какъ число 60 обладаетъ массой дѣлителей и, слѣдов., рѣже приводитъ къ дробямъ, чѣмъ большинство другихъ чиселъ, и позволяетъ дѣлать много упрощеній. Халдеи примѣняли шестидесятеричный счетъ вездѣ: и въ торговыхъ дѣлахъ, и въ научныхъ выкладкахъ, особенно же въ любимой своей наукѣ, которая многимъ обязана ихъ трудамъ,—въ астрономіи. Привычка къ числу 60 сама собой перешла и на дроби, и вотъ у халдеевъ явились шестидесятеричныя дроби, т.-е. со знаменателемъ 60, 3600 = 60. 60, 216000 = 60. 60. 60. Эти дроби примѣнены были въ астрономіи къ дѣленію времени, такъ что часъ сталъ дѣлиться на 60 равныхъ частей (минутъ), минута на 60 секундъ, секунда на 60 терцій и т. д. Всѣ простыя дроби халдеями обыкновенно приводились въ шестидесятыя доли и даже, напр., ⅔ они выражали не иначе, какъ черезъ 40/ 60.
Отъ халдеевъ шестидесятеричныя доли перешли къ индусамъ и арабамъ, и также къ грекамъ. Особенно онѣ были разработаны греческими учеными, жившими въ Александріи въ первые вѣка по Р. X. Знаменитый астрономъ Клавдій Птоломей (во II в. по Р. X.), система котораго держалась болѣе тысячи лѣтъ и признавалась въ свое время геніальнымъ твореніемъ, писалъ, обыкновенно, шестидесятеричныя дроби безъ знаменателя. Для этого онъ цѣлыя числа подчеркивалъ горизонтальной чертой, шестидесятыя доли отмѣчалъ значком ′, 3600-ыя значком ″, 216000-ыя доли значкомъ ‴ и т. д., смотря по ихъ разряду. И это дѣлалось не только при измѣреніи времени и при градусахъ дуги, но и въ мѣрахъ длины и въ другихъ мѣрахъ. Такъ, напр., Птоломей выражаетъ сторону правильнаго вписаннаго десятиугольника черезъ — 37 4′ 55″, при діаметрѣ круга, равномъ 120. Это значитъ, что если діаметръ составляетъ 120, то сторона равняется
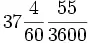
такихъ же единицъ (по порядку, принятому въ настоящее время въ геометріи, сторону эту можно выразить въ десятичныхъ дробяхъ чрезъ 0,30902, при діаметрѣ, равномъ единицѣ).
Горизонтальная черта, которой подчеркивались цѣлыя чиcла, была замѣнена впослѣдствіи знакомъ °, и самимъ долямъ были присвоены названія: минуты, секунды, терціи и т. д. Что значатъ эти слова? Минута значитъ «доля», и долго послѣ Птоломея, болѣе тысячи лѣтъ, всевозможныя доли всегда назывались минутами (minutae). Къ слову минута присоединялось, обыкновенно, слово прима (prima), и выраженіе «minuta prima» обозначало первыя доли, иначе сказать доли перваго порядка, т.-е. со знаменателемъ 60. Далѣе шли доли со знаменателемъ 3600, онѣ назывались минутами секундами, т.-е. долями второго порядка, такъ какъ 3600 = 60·60. Потомъ слѣдовали минуты терціи, доли третьяго порядка, у которыхъ знаменатель 60·60·60.
Читать дальше
![Всеволод Беллюстин Как постепенно дошли люди до настоящей арифметики [без таблиц] обложка книги](/books/299296/vsevolod-bellyustin-kak-postepenno-doshli-lyudi-do-na-cover.webp)
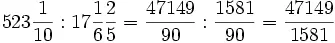
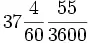


![Тимонг Лайтбрингер - Людям Настоящего [поэзия]](/books/274501/timong-lajtbringer-lyudyam-nastoyachego-poeziya-thumb.webp)
![Тимонг Лайтбрингер - Людям Настоящего [проза]](/books/276605/timong-lajtbringer-lyudyam-nastoyachego-proza-thumb.webp)






