Сергей Дориченко - 25 этюдов о шифрах

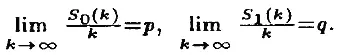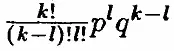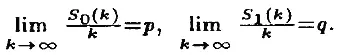
Контрольный вопрос . Пусть мы случайным образом подбрасываем монету, причём p = q =½ и первые сто членов соответствующей последовательности равны 1 (100 раз подряд выпала решка). Чему равно вероятность того, что 101-ым членом этой последовательности снова будет 1?

Правильный ответ на этот вопрос : ½. Так как q =½, а случайность нашей последовательности как раз и означает, что каждый очередной её член равен 1 с вероятностью q независимо от того, какими были предыдущие её члены.

Обычно последовательности, с которыми на практике приходится иметь дело, вообще говоря, не строго случайные (неслучайные). Изучение случайных и неслучайных двоичных последовательностей имеет важное значение для криптографии. Например, выявление закономерностей в шифрованных сообщениях очень полезно при вскрытии шифра (см. этюд 2.7). В этюде 2.5 вы также узнаете, что для построения абсолютно стойкого шифра необходимо уметь получать совершенно случайный ключ.

Задачам различения случайной и неслучайной последовательностей, а также выявления закономерностей в неслучайных последовательностях посвящено много исследований в различных областях математики. Так, например, один из основных разделов математической статистики — это проверка статистических гипотез , в котором, в частности, разрабатываются методы различения гипотез о природе и характеристиках наблюдаемых последовательностей. Другой пример — это активно изучаемый в современной теоретической криптографии гипотетический объект — псевдослучайный генератор . При изучении этого объекта используются многочисленные результаты теории сложности алгоритмов и вычислений. Говоря неформально, псевдослучайный генератор вырабатывает такие последовательности, которые трудно отличить от случайных и из которых трудно извлечь закономерности. Строгие определения необходимых понятий выходят за рамки нашей книги.

Близким по духу, но более простым и хорошо известным, особенно для программистов, является такой объект, как датчик случайных чисел . Это — некоторое устройство или программа, которая вырабатывает псевдослучайные последовательности . Псевдослучайные последовательности в некоторых ситуациях считают неотличимыми от случайных, причем для разных ситуаций и задач подбирают подходящие датчики. Чем более сильные требования накладываются на случайность вырабатываемых последовательностей, тем более сложным является соответствующий датчик случайных чисел. Многие шифрмашины можно считать датчиками случайных чисел, удовлетворяющими очень высоким требованиям на качество вырабатываемых последовательностей.

Опишем, например, один простейший датчик, предложенный в 1949 году Д.Х. Лемером и в дальнейшем получивший название линейного конгруэнтного метода . Для заданного начального числа a 0он вырабатывает бесконечную последовательность натуральных чисел { a k } по следующему рекуррентному закону :

a k = d + a k −1∙ ℓ (mod N ).

Здесь параметры датчика d , ℓ , N — некоторые целые числа. Запись a = b (mod N ), вообще говоря, означает, что a − b делится на число N ; в данном случае в качестве a k берется остаток от деления d + a k −1∙ ℓ на N .

Поскольку все члены последовательности { a k } — неотрицательные целые числа, не превосходящие N −1, то среди них найдутся два одинаковых, скажем a i и a i + t . Тогда, как легко видеть, a i = a i + t для k ≥ i , т.е. последовательность — периодическая с длиной периода t . Конечно, периодичность не вполне согласуется с нашими представлениями о случайности, но, оказывается, можно подбирать такие параметры датчика, чтобы период был достаточно большим и у последовательности были многие признаки случайности.

Следует отметить, что «хорошей во всех отношениях случайной последовательности» практически не существует: насколько «хорошей» является случайная последовательность, зависит от ее назначения.

Подумайте сами :

1. Докажите следующее утверждение: вероятность того, что при k подбрасываниях кривой монеты ℓ раз выпадет орёл, равняется:

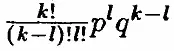
2. Придумайте такие числа d , ℓ и N , чтобы N было не слишком маленьким и длина периода последовательности, полученной линейным конгруэнтным методом, была близка к N .