Е. Миркес - Учебное пособие по курсу «Нейроинформатика»

где F ij = G mij -1- b ic j / b 0. Поскольку матрица, обратная к симметричной, всегда симметрична получаем c i / b 0= - b i / b 0при всех i . Так как b 0≠ 0 следовательно b i= -c i .

Обозначим через dвектор (( x 1, x m +1), …, ( x m , x m +1)), через b— вектор ( b 1, …, b m ). Используя эти обозначения можно записать b= G m -1 d, b 0= ( x m +1, x m +1)-( d, b), b 0= ( x m +1, x m +1)-( d, b). Матрица G m+1 -1записывается в виде

Таким образом, при добавлении нового эталона требуется произвести следующие операции:

1. Вычислить вектор d( m скалярных произведений — mn операций, mn ≤ n ²).

2. Вычислить вектор b(умножение вектора на матрицу — m ² операций).

3. Вычислить b 0(два скалярных произведения — m + n операций).

4. Умножить матрицу на число и добавить тензорное произведение вектора bна себя (2 m ² операций).

5. Записать G m+1 -1.

Таким образом эта процедура требует m + n + mn +3 m ² операций. Тогда как стандартная схема полного пересчета потребует:

1. Вычислить всю матрицу Грама ( nm ( m +1)/2 операций).

2. Методом Гаусса привести левую квадратную матрицу к единичному виду (2 m ³+ m ²- m операций).

3. Записать G m+1 -1.

Всего 2 m ³+ m ²– m + nm ( m +1)/2 операций, что в m раз больше.

Используя ортогональную сеть (6), удалось добиться независимости способности сети к запоминанию и точному воспроизведению эталонов от степени коррелированности эталонов. Так, например, ортогональная сеть смогла правильно воспроизвести все буквы латинского алфавита в написании, приведенном на рис. 1.

Основным ограничением сети (6) является малое число эталонов — число линейно независимых эталонов должно быть меньше размерности системы n .

Для увеличения числа линейно независимых эталонов, не приводящих к прозрачности сети, используется прием перехода к тензорным или многочастичным сетям [75, 86, 93, 293].

В тензорных сетях используются тензорные степени векторов. k- ой тензорной степенью вектора x будем называть тензор x ⊗k, полученный как тензорное произведение k векторов x.

Поскольку в данной работе тензоры используются только как элементы векторного пространства, далее будем использовать термин вектор вместо тензор. Вектор x ⊗kявляется n k -мерным вектором. Однако пространство L ({x ⊗k}) имеет размерность, не превышающую величину , где — число сочетаний из p по q . Обозначим через {x ⊗k} множество k- х тензорных степеней всех возможных образов.

Теорема. При k в множестве {x ⊗k} линейно независимыми являются векторов. Доказательство теоремы приведено в последнем разделеданной главы.

Небольшая модернизация треугольника Паскаля, позволяет легко вычислять эту величину. На рис. 2 приведен «тензорный» треугольник Паскаля. При его построении использованы следующие правила:

1. Первая строка содержит двойку, поскольку при n= 2 в множестве X всего два неколлинеарных вектора.

2. При переходе к новой строке, первый элемент получается добавлением единицы к первому элементу предыдущей строки, второй — как сумма первого и второго элементов предыдущей строки, третий — как сумма второго и третьего элементов и т. д. Последний элемент получается удвоением последнего элемента предыдущей строки.

Рис. 2. “Тензорный” треугольник Паскаля

В табл. 1 приведено сравнение трех оценок информационной емкости тензорных сетей для некоторых значений n и k. Первая оценка — n k — заведомо завышена, вторая — — дается формулой Эйлера для размерности пространства симметричных тензоров и третья — точное значение.

Таблица 1.

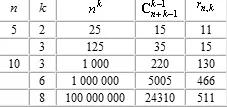
Как легко видеть из таблицы, уточнение при переходе к оценке r n,k является весьма существенным. С другой стороны, предельная информационная емкость тензорной сети (число правильно воспроизводимых образов) может существенно превышать число нейронов, например, для 10 нейронов тензорная сеть валентности 8 имеет предельную информационную емкость 511.