Мартин Гарднер - Математические головоломки и развлечения

Когда наша модель имеет вид двойной ленты, два ее края идут параллельно друг другу и описывают два полных оборота. Представим себе, что эти края склеены, а сама лента сделана из тонкой резины. Тогда мы получим трубку, которую можно раздуть и превратить в тор (так топологи называют обычный бублик). Склеенные края образуют на поверхности тора замкнутую кривую: намотанную на тор спираль, состоящую из двух витков. Это означает, что, разрезав тор вдоль такой кривой, мы получим двойной лист Мёбиуса — это не что иное, как обыкновенная лента, концы которой перед тем, как их склеить, перекрутили четыре раза (каждый поворот — на 180°). Тор можно превратить в ленту, концы которой повернуты относительно друг друга на любое четное число полуоборотов, но его нельзя разрезать так, чтобы он превратился в ленту, которую перекрутили нечетное число раз. Это связано с тем, что тор — поверхность двусторонняя. Из лент двусторонними являются лишь те, которые перекручены четное число раз (напомним, что, перекручивая ленту, мы каждый раз поворачиваем ее концы на 180° относительно друг друга). Двусторонние поверхности можно получить, разрезая односторонние, хотя обратное невозможно. Если же мы хотим получить односторонние ленты (ленты с нечетным числом перекручиваний на пол-оборота каждое), разрезая поверхность без края, то нам следует обратиться к разрезанию бутылки Клейна.

Бутылка Клейна представляет собой замкнутую одностороннюю поверхность без края, и ее можно рассечь на два листа Мёбиуса, каждый из которых будет зеркальным отображением другого.

Обычный лист Мёбиуса получают, склеивая концы перекрученной на пол-оборота ленты. Можно ли растянуть лист Мёбиуса так, чтобы его край принял форму треугольника? Оказывается, можно.

Первым, кто придумал такую модель, был Брайан Таккерман, один из четырех основоположников искусства складывать флексагоны (см. главу 1). На рис. 29 показано, как следует разрезать, сложить и склеить лист бумаги, чтобы построить модель Таккермана.

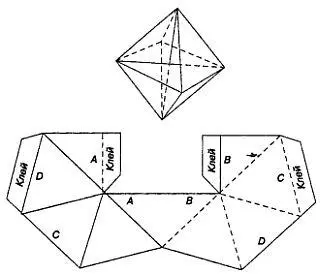
Рис. 29Лист Мёбиуса с треугольным краем, придуманный Брайаном Таккерманом. Перечертив изображенную на этом рисунке выкройку в увеличенном масштабе, можно склеить модель, показанную вверху.

Для изготовления модели необходимо проделать следующие операции: 1) вырезать выкройку фигуры из бумаги; 2) перегнуть ее вдоль сплошных линий так, чтобы ребро сгиба было обращено острием вверх; 3) перегнуть выкройку вдоль пунктирных линий так, чтобы острие сгиба было обращено вниз; 4) намазав клеем четыре клапана, склеить выкройку так, чтобы отрезки, обозначенные одинаковыми буквами, совпали. Сплошные линии на поверхности получившегося многогранника образуют треугольный край листа Мёбиуса.

Поверхности могут быть не только односторонними и двусторонними. С точки зрения топологии, они могут отличаться друг от друга числом своих краев и их устройством. Поскольку ни число краев, ни их структуру нельзя изменить, деформируя поверхность, они называются топологическими инвариантами. Рассмотрим поверхности, имеющие не более двух краев. Будем считать, что краем могут быть либо простые замкнутые кривые, либо кривые, имеющие форму обычного простого узла. При таком предположении можно указать следующие 16 типов поверхностей (сюда не входят такие поверхности без края, как сфера, тор и бутылка Клейна):

Односторонние поверхности с одним краем

1. Край имеет форму простой замкнутой кривой.

2. Край «завязан узлом».

Двусторонние поверхности с одним краем

3. Край — простая замкнутая кривая.

4. Край «завязан узлом».

Односторонние поверхности с двумя краями

5. Оба края — простые замкнутые кривые, не зацепленные друг за друга.

6. Оба края — простые замкнутые кривые, зацепленные друг за друга.

7. Оба края завязаны в узел, но не зацеплены друг за друга.

8. Оба края завязаны в узел и зацеплены друг за друга.

9. Один край простой, другой завязан узлом; между собой края не зацеплены.

10. Один край простой, другой завязан узлом; края зацеплены.

Двусторонние поверхности с двумя краями

11. Оба края — простые замкнутые кривые, не зацепленные друг за друга.

12. Оба края — простые замкнутые кривые, зацепленные друг за друга.

13. Оба края завязаны в узел, между собой не зацеплены.

14. Оба края завязаны в узел и зацеплены друг за друга.