Мартин Гарднер - Математические головоломки и развлечения

Даже если бы жрецы работали не покладая рук, днем и ночью, перенося каждую секунду по одному кольцу, чтобы закончить работу, им понадобились бы многие миллионы тысячелетий.

(Получившееся число не является простым, но если число колец увеличить до 89, 107 или 127, то в каждом случае нужное число перемещений будет простым. Эти числа называются числами Мерсенна: простые числа, которые можно представить в виде 2 n— 1.

Сам Люка был первым, кто установил, что число 2 127— 1 простое.

Это огромное 39-значное число было самым большим из всех известных вплоть до 1952 года простых чисел. В 1952 году с помощью большой электронно-вычислительной машины было найдено пять новых чисел Мерсенна. Самое большое из них имеет вид 2 2281— 1.

Существует много аргументов в пользу того, что число 2 8191— 1 также простое, но пока это не доказано.)

Головоломку «Ханойская башня» легко сделать из восьми картонных квадратиков постепенно увеличивающегося размера (с тем же успехом можно взять игральные карты от туза до восьмерки), которые нужно перекладывать между тремя отметками на листе бумаги. Если эти отметки образуют треугольник, то задача решается для любого числа колец следующим простым способом. Начнем с самого маленького квадрата и переложим его на любую отметку. В дальнейшем этот квадратик нужно перемещать в том же направлении, что и при первом перекладывании. Затем произведем единственно возможное перемещение оставшихся квадратов, после чего снова переложим самый маленький квадрат и т. д. (Интересно заметить, что, перенумеровав «кольца» по порядку, мы добьемся неожиданного эффекта: четные квадраты будут перемещаться из одной вершины треугольника в другую в одном направлении, а нечетные— в противоположном направлении.)

Что же общего у «Ханойской башни» с игрой, придуманной Гамильтоном? Чтобы понять, как эти две знаменитые головоломки связаны между собой, рассмотрим сначала пирамиду из трех колец, на которых по порядку сверху вниз нанесены буквы А, В и C. Следуя описанному выше алгоритму решения задачи, кольца нужно перемещать в следующей последовательности: ABAC ABA.

Обозначим теперь через А, В и С три оси координат, выбранные в направлениях, параллельных осям правильного шестигранника — куба (на рис. 25 — слева).

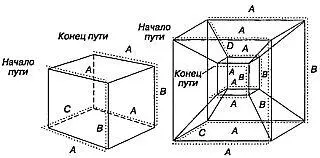
Рис. 25Путь Гамильтона, проходящий по ребрам куба (слева). Оси координат выбраны параллельно ребрам куба и обозначены буквами А, В и С. Путь последовательно идет по направлениям осей ABAC ABA. Справа показан путь Гамильтона, проходящий по ребрам четырехмерного куба, спроектированного в трехмерное пространство. Оси четырех координат гиперкуба обозначены буквами А, В, С и D. Путь последовательно идет по направлениям осей ABACABADABACABA. В том же порядке нужно перекладывать четыре диска в «Ханойской башне».

Если, обходя ребра куба, мы будем двигаться по направлениям этих осей в последовательности ABAC ABA, то наш маршрут окажется одним из гамильтоновых путей! Кроув заметил, что этот результат допускает обобщение: порядок перекладывания дисков при игре в «Ханойскую башню» в точности совпадает с порядком, в котором мы проходили направления координатных осей при следовании по гамильтонову пути на n-мерном кубе.

Поясним сказанное на еще одном примере. Хотя мы и не можем изготовить модель четырехмерного куба (называемого также гиперкубом или тессерактом), тем не менее ребра четырехмерного куба можно спроецировать на трехмерную модель, изображенную на рис. 25. Сеть ребер этой модели топологически эквивалентна сети ребер гиперкуба. Обозначим оси координат буквами А, В, С и D. Координата D означает расстояние, проходимое по ребрам гиперкуба. Тогда порядок перекладывания для пирамиды из четырех колец будет таким ABACABADABACABA. Следуя по ребрам гиперкуба в направлениях, указанных этой последовательностью, мы пройдем гамильтонов путь. Аналогичные рассуждения показывают, что перекладывание пяти колец соответствует пути Гамильтона, проложенному по ребрам пятимерного гиперкуба, перекладывание шести колец — гамильтонову пути, проходящему по ребрам шестимерного гиперкуба, и т. д.

* * *

Доказательство того, что п колец можно перенеси с одного колышка на другой в (2 n— 1) приемов, довольно простое и может послужить хорошим упражнением на применение метода полной математической индукции. [13] Mathematics Teacher: 44.-1951, p. 505; 45.-1952, p. 522. Задача легко обобщается на любое число колышков.