Мартин Гарднер - Математические головоломки и развлечения

Эта игра упоминается у Овидия в книге III «Искусства любви» в числе тех игр, которыми поэт советует овладеть женщине, если она хочет привлечь к себе внимание мужчин в обществе. Игра в крестики и нолики была известна в Англии еще в 1300 году под названием «Танец трех мужчин», от которого пошли «танцы» девяти, одиннадцати и двенадцати мужчин; в Америке последний вариант по сей день называется «мельница». Поскольку первый игрок, начиная с центра, наверняка выигрывает, то такое начало не сулит ничего интересного и обычно им не пользуются. Это ограничение при рациональной тактике приводит к ничьей, но обе стороны могут поставить противнику уйму потенциальных ловушек.

В одном из вариантов игры разрешается передвигаться на соседние клетки вдоль двух главных диагоналей. Дальнейшее видоизменение игры (приписываемое американским индейцам) допускает перемещение любой фишки на одну клетку в любом направлении (например, с клетки 2 можно передвинуться на клетку 4). В первом варианте тот, кто делает первый ход, может добиться победы, если начнет с центра, но второй вариант, по-видимому, всегда можно свести вничью. В игре без всяких ограничений, называемой во Франции «les pendus » («повешенные»), фишку разрешается передвигать на любую свободную клетку. Эта игра при разумной тактике также заканчивается вничью.

Известно много разновидностей крестиков и ноликов, в которых игра ведется на доске размером 4 клетки на 4. У каждого игрока имеется по четыре фишки, и их нужно попытаться выстроить в один ряд. В шестидесятые годы появилась игра «тико» — разновидность крестиков и ноликов, для которой нужна доска размером пять клеток на пять. Каждый из игроков по очереди выставляет свои четыре фишки, а затем передвигает их на одну клетку в любом направлении. Выигрывает тот, кто сумеет либо поставить свои четыре фишки в ряд (по горизонтали, вертикали или диагонали), либо выстроит их в виде квадрата на четырех клетках с общей вершиной.

Играть в крестики и нолики можно и без фишек, от этого игра не становится менее увлекательной. Рассмотрим, например, игру в крестики и нолики «наоборот» — тоу-так-тик (это название предложил М. Шоделл). Играют в нее, как в обычные крестики и нолики, но тот, кто первым закончит ряд из трех знаков, не выигрывает, а проигрывает. В игре тоу-так-тик у второго игрока имеется бесспорное преимущество. Первый может закончить вничью, лишь заняв первым же ходом центр, а в дальнейшем повторив по симметрии все ходы противника.

В последние годы появилось несколько трехмерных игр типа крестиков и ноликов. В них играют на кубических досках, а выигрывает тот, кому удается занять подряд все клетки по горизонтали, вертикали или диагонали в любом сечении куба, параллельном его грани, или на четырех главных диагоналях куба. Если куб имеет размер 3 х 3 х 3, то первый игрок побеждает без труда. Интересно заметить, что эта игра никогда не может закончиться вничью, ибо у первого игрока имеется четырнадцать разных ходов. Сделать же все четырнадцать ходов, не заполнив при этом одного из рядов по вертикали, горизонтали или диагонали, просто невозможно. Гораздо интереснее играть на кубической доске размером 4x4x4. Здесь лишь при разумной тактике ничьей может не быть.

Предлагались и другие варианты игры на кубических досках.

Так, А. Барнерт придумал игру, в которой победителем считается тот, кто заполнит своими фишками клетки в любом сечении куба, параллельном одной из граней, или в шести главных диагональных плоскостях. П. Парке и Р. Саттен еще в 1941 году изобрели интересную игру на кубической доске размером 3x3x3 клетки, в которой выигрывает тот, кто сумеет занять два пересекающихся ряда. Клетку, стоящую на пересечении двух рядов, правила игры разрешают занимать в последнюю очередь. Поскольку занявший центральную клетку куба заведомо обеспечивает себе победу, этот ход разрешается лишь в двух случаях: а) если им достигается победа, то есть если все остальные клетки двух рядов, пересекающихся в центре куба, уже заняты фишками данного игрока; б) если, заняв эту клетку, играющий мешает своему противнику следующим ходом выиграть партию.

В четырехмерные крестики и нолики играют на воображаемой гиперкубической доске, поделив ее на двумерные квадраты. Например, гиперкуб 4x4x4x4 выглядит так, как показано на рис. 19.

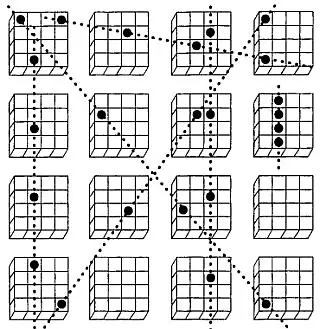
Рис. 19 Четырехмерные крестики и нолики. Пунктиром показаны некоторые ходы, приводящие к выигрышу.