Мартин Гарднер - Математические головоломки и развлечения

6. Решение головоломки опирается на маленькую хитрость в расписании поездов. Оно составлено так, что поезд, следующий в Бронкс, всегда прибывает на минуту позже бруклинского, в то время как интервалы движения обоих поездов одинаковы — 10 минут.

Отсюда ясно, что поезд в Бронкс прибудет раньше бруклинского только в том случае, если молодой человек явится на вокзал в течение этого минутного интервала. В любое же другое время (то есть в течение девятиминутного интервала) бруклинский поезд будет прибывать первым. Поскольку молодой человек приходит в совершенно произвольные моменты времени, он с вероятностью 0,9 отправляется в Бруклин.

7. Разрезать куб менее чем шестью распилами нельзя. Это становится ясным, если вспомнить, что у куба шесть граней. Каждый распил означает проведение плоскости, то есть при каждом распиле появляется не более одной новой грани куба. Чтобы выпилить маленький кубик в самом центре большого куба (это единственный кубик, у которого вначале нет ни одной готовой грани), нужно провести шесть распилов. Эту задачу придумал Ф. Хоуторн.

Кубы размером 2х2х2 и ЗхЗхЗ — единственные в том смысле, что, как бы вы ни складывали их части, прежде чем произвести очередной распил (разумеется, если при этом каждая часть куба где-то распиливается), все равно, пока кубы не распадутся на единичные кубики, первый придется пилить три раза, а второй — шесть.

Для куба 4x4x4 понадобится провести девять распилов, если его части все время будут составлять куб. Переставляя их перед каждым распилом, можно уменьшить число последних до шести.

Складывая куски куба, нужно следить за тем, чтобы каждый из них распиливался как можно ближе к середине, тогда число распилов будет минимальным. В общем случае для куба n х n х n минимальное число распилов равно Зк , где к определяется неравенством

2 k>= n > 2 k-1

В общем виде эта задача была поставлена Л. Р. Фордом и Д. Р. Фулкерсоном. Однако она представляет собой лишь частный случай более общей задачи, опубликованной Л. Мозером, о минимальном числе распилов, которые необходимо произвести, чтобы разрезать прямоугольный параллелепипед размером а х b х с на единичные кубики.

Ю. Дж. Патцер и Р. В. Лоуэн в своей работе «Об оптимальном способе распиливания прямоугольного параллелепипеда на единичные кубы [9] Putzer E. J., Lowen R. W. On the Optimum Method of Cutting a Rectangular Box into Unit Cubes: Convair Scientific Research Laboratory. — San Diego: 1958. пошли еще дальше. Они рассматривают n -мерные кирпичи с целыми сторонами, которые надо разделить минимальным числом плоских распилов на единичные гиперкубы. Авторы считают, что трехмерная задача «может найти применение в сыроваренной и сахарной промышленности».

8. Пассажир, приехавший необычно рано, шел пешком 55 мин, прежде чем его подобрала жена. Если они приехали домой на 10 мин раньше обычного, это значит, что жена выиграла 10 мин от времени своей обычной поездки на станцию и обратно или 5 мин от времени поездки на станцию. Следовательно, она встретила мужа за пять минут до того момента (пять часов), когда обычно сажала его в машину, то есть в 4 ч 55 мин. Он вышел в четыре часа, поэтому шел 55 мин. Скорость пешехода, скорость машины и расстояние от дома до станции для решения задачи не нужны. Если вы пытались подобрать эти величины, вам, наверное, показалось, что задача чересчур сложна.

Некоторые читатели заметили, что решение задачи намного упрощается, если нарисовать график движения (рис. 16).

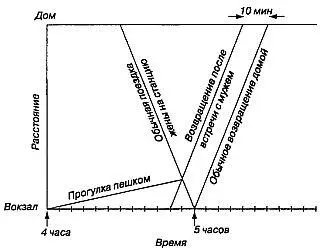
Рис. 16 График к задаче о раннем пассажире.

По горизонтальной оси отложено время, по вертикальной — расстояние.

Из графика видно, что жена могла выехать из дому самое большее на 10 мин раньше, чем нужно, чтобы вовремя попасть к поезду.

Нижний предел продолжительности прогулки мужа (50 мин) достигается лишь тогда, когда жена выезжает из дому ровно на десять минут раньше обычного и либо сама едет с бесконечно большой скоростью (в этом случае муж прибывает домой в тот же момент, в какой она выезжает из дому), либо муж идет с бесконечно малой скоростью (в этом случае жена встречает его у самого вокзала, откуда он вышел за 50 мин до встречи, поскольку за эти 50 мин муж так и не сдвинулся с места). «Ни одно из этих предположений, — пишет профессор Д. У. Вайзер, приславший одно из лучших решений задачи с подобным анализом, — не следует считать ошибочным: ни мастерское вождение машины женой, ни странное поведение мужа, который битый час не трогается с места, поровнявшись с пивной».