Мартин Гарднер - Математические головоломки и развлечения

Избитый ответ «белого» основан на неявном предположении, что исходной и конечной точкой замкнутого маршрута непременно должен быть Северный полюс. Не так давно было сделано открытие, что Северный полюс — отнюдь не единственная точка, удовлетворяющая всем условиям этой задачи!

Можете ли вы указать еще какую-нибудь точку земного шара, из которой можно было бы пройти один километр на юг, один километр на восток, один километр на север и снова оказаться в самом начале пути?

2. Покер.Двое играют в покер по следующим необычным правилам. Колоду из 52 карт они раскладывают на столе так, что могут видеть масти и значения всех карт. Первый игрок выбирает любые пять карт, второй делает то же самое, но его выбор ограничен лишь теми картами, которые остались лежать на столе. После этого первый игрок может либо оставить у себя на руках прежние пять карт, либо взять со стола новые карты (не больше пяти) и, выбрав из всех оказавшихся у него на руках карт любые пять, остальные отложить в сторону. Второй игрок вправе поступать точно таким же образом. Выигрывает тот, кто сумеет набрать пятерку карт с наибольшим числом очков. Все масти считаются одинаковыми, то есть флеши [8] Флеш — четыре последовательные карты одной масти. разной масти различаются по очкам лишь в том случае, если они состоят из разных карт. Через несколько партий игроки замечают, что первый игрок всегда выигрывает, если он правильно сделает свой первый ход.

Какие пять карт должен выбрать первый игрок в начале игры?

3. Изуродованная шахматная доска.Для этой задачи нам потребуются шахматная доска и 32 кости домино. Размер каждой кости должен быть таким, чтобы она закрывала ровно две клетки доски, тогда 32 костями можно покрыть все 64 клетки.

Предположим теперь, что две угловые клетки, расположенные на концах «белой» диагонали (рис. 13), выпилены и одной кости домино нет.

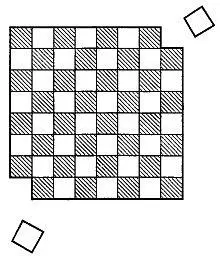
Рис. 13 Шахматная доска с выпиленными углами.

Можно ли так расположить оставшиеся кости (их 31), чтобы они полностью покрыли все 62 клетки изуродованной шахматной доски? Если можно, то как? Если нельзя, то докажите, что это действительно невозможно.

4. На распутье.То, о чем мы сейчас расскажем, представляет собой новый вариант давно известного типа логических головоломок. Некий логик решил провести свой отпуск в путешествии по южным морям. Однажды он оказался на острове, который, как водится в задачах этого рода, населяли племя лжецов и племя правдивых туземцев. Члены первого племени всегда лгали, члены второго — всегда говорили только правду. Путешественник дошел до места, где дорога раздваивалась, и вынужден был спросить у оказавшегося поблизости туземца, какая из двух дорог ведет в деревню. Узнать, кем был встреченный туземец—лжецом или правдивым человеком, — путешественник не мог. Все же, поразмыслив, логик задал ему один-единственный вопрос и, получив ответ, узнал, по какой дороге следует идти. Какой вопрос задал путешественник?

5. Перепутанные таблички. Представьте себе, что у вас есть три коробки. В одной лежат два черных шара, во второй — два белых и в третьей — один черный шар и один белый. На коробках в соответствии с их содержимым были надписи ЧЧ, ЧБ и ББ, но кто-то их перепутал, и теперь на каждой коробке стоит надпись, не соответствующая содержимому. Чтобы узнать, какие шары лежат в каждой из трех коробок, разрешается вынимать по одному шару из коробки и, не заглядывая внутрь, возвращать его обратно. Какое минимальное число шаров нужно вынуть, чтобы с уверенностью определить содержимое всех коробок?

6. В Бронкс или Бруклин?Один молодой человек живет в Манхэттене возле станции метро. У него есть две знакомые девушки. Одна из них живет в Бруклине, вторая — в Бронксе. Когда он едет к девушке из Бруклина, то садится в поезд, подходящий к платформе со стороны центра города. Когда же едет к девушке из Бронкса, то садится в поезд, идущий в центр. Поскольку обе девушки нравятся ему одинаково, он просто садится в тот поезд, который приходит первым. Таким образом, в выборе, куда ехать, он полагается на случай. Молодой человек приходит на станцию каждую субботу в разное время. И в Бруклин и в Бронкс поезда ходят с одинаковым интервалом в 10 минут. Тем не менее по каким-то непонятным причинам большую часть времени он проводит с девушкой из Бруклина; в среднем из каждых десяти поездок девять приходятся на Бруклин. Попробуйте догадаться, почему у Бруклина такой огромный перевес.