Мартин Гарднер: Математические головоломки и развлечения

При этом длина полоски сократится вдвое и станет равной длине гексагексафлексагонной полоски. Затем скрученную полоску нужно сложить точно таким образом, как если бы вы складывали гексагексафлексагон. В результате получится додекагексафлексагон.

Экспериментируя с флексагонами высоких порядков, полезно иметь в виду удобное правило: число слоев бумаги в двух соседних треугольных секциях всегда равно числу поверхностей данного флексагона. Интересно также отметить, что если каждую поверхность флексагона пометить каким-нибудь числом или символом и этот символ поставить на всех треугольниках, принадлежащих данной поверхности, то чередование символов на развернутой полоске будет обладать трехкратной периодичностью. Например, на лицевой и обратной сторонах развертки гексагексафлексагона, изображенного на рис. 2, цифры будут располагаться в такой последовательности:

Аналогичное разделение символов на три группы характерно для всех гексагексафлексагонов, но у флексагонов нечетного порядка символы в одной из трех групп расположены в обратном порядке по сравнению с двумя остальными группами.

Из многих сотен писем, полученных мной в связи со статьей о флексагонах, я считаю наиболее забавными два. В свое время они были опубликованы в Scientific American. Вот они.

Уважаемая редакция!

Меня прямо-таки потрясла статья «Флексагоны», опубликованная в декабрьском номере вашего журнала (за 1956 год).

Провозившись каких-нибудь шесть или семь часов, я с помощью сотрудников нашей лаборатории в конце концов сумел правильно склеить гексагексафлексагон. С тех пор вся наша лаборатория не перестает удивляться.

Сейчас мы встали перед проблемой. Как-то утром один из наших сотрудников, занимаясь от нечего делать складыванием гексагексафлексагона, не заметил, как кончик его галстука попал внутрь этой игрушки. При каждом последующем перегибании галстук несчастного все больше и больше втягивался внутрь флексагона. После шестого перегибания исчез сам сотрудник.

Разумеется, мы тут оке начали лихорадочно перегибать флексагон, но так и не обнаружили никаких следов нашего товарища, зато мы нашли шестнадцатую поверхность гексагексафлексагона.

Возникает вопрос: должна ли вдова исчезнувшего сотрудника получить компенсацию за все время его отсутствия или же мы можем с полным основанием сразу считать его умершим? Ждем вашего совета.

НЕЙЛ АПТЕГРОУВ

Лаборатории Аллена В. Дюмона

Клифтон, штат Нью-Джерси

Сэр!

Письмо об исчезновении внутри гексагексафлексагона сотрудника Лабораторий Аллена В. Дюмона, напечатанное в мартовском выпуске вашего журнала, помогло нам решить одну загадку.

Однажды, занимаясь на досуге складыванием гексагексафлексагона самой последней модели, мы заметили, что из него торчит кусочек какой-то пестрой материи. При последующих перегибаниях флексагона из него показался незнакомец, жующий резинку.

К сожалению, он был очень слаб и из-за частичной потери памяти не мог объяснить нам, каким образом оказался внутри флексагона. Наша национальная диета из овсянки, хэггиса [6] Хэггис — шотландское национальное блюдо, которое готовится из овечьей или телячьей требухи и овсяной муки, приправленных луком и перцем. и виски поправила его здоровье. Он стал всеобщим любимцем и откликается на имя Экклз.

Нас интересует, нужно ли нам вернуть его и если да, то каким способом? К сожалению, Экклза бросает в дрожь при одном лишь виде гексагексафлексагона, и он решительно отказывается «складываться».

РОБЕРТ М. ХИЛЛ

Королевский колледж науки и техники

Глазго, Шотландия

Магические квадраты занимают воображение математиков уже более двух тысячелетий. В традиционном магическом квадрате суммы чисел в каждом столбце, каждом ряду и по каждой диагонали одинаковы. Совершенно иной тип магического квадрата изображен на рис. 8.

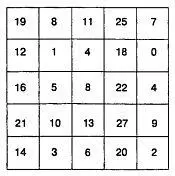
Рис. 8

На первый взгляд может показаться, что он составлен без всякой системы и числа в нем расположены случайным образом.

Тем не менее этот квадрат обладает магическим свойством, вызывающим удивление не только у человека, далекого от науки, но и у профессионала-математика.

Это свойство лучше всего демонстрировать с помощью пяти монет и 20 бумажных фишек. Попросите кого-нибудь выбрать любое из чисел, вписанных в клетки квадрата. Положите на это число монету и закройте фишками все остальные числа, стоящие в одной строке и одном ряду с выбранным.