О. ОРЕ: Приглашение в теорию чисел

Но сумма всех чисел от 1 до n 2равна

1 + 2 +… + n 2= ½ ( n 2+ 1) n 2,

что следует из формулы для суммы n членов арифметической прогрессии. Так как

n s = ½ ( n 2+ 1) n 2,

то

s = ½ n ( n 2+ 1). (1.5.1)

Таким образом, если число n задано, то число s определено. Магические квадраты могут быть построены для любого числа n , которое больше 2; читатель легко может убедиться, что их не существует для n = 2.

Во времена средневековья странные свойства этих квадратов считались волшебными и поэтому магические квадраты служили талисманами, защищающими тех, кто их носил, от многих несчастий. Часто воспроизводится магический квадрат, присутствующий на знаменитой гравюре Альбрехта Дюрера «Меланхолия» (она помещена на фронтисписе нашей книги). Этот квадрат воспроизведен с большим увеличением на рис. 9; при этом мы получили также возможность увидеть, как во времена Дюрера изображались цифры. Средние числа в последней строке изображают год, — 1514, в котором, как мы знаем, была создана эта гравюра. Возможно, что Дюрер, положив в основу именно эти числа, нашел остальные методом проб и ошибок. Можно доказать, что при n = 3 имеется лишь один магический квадрат, а именно квадрат, изображенный на рис. 7. Докажем этот факт. Для этого напишем числовой квадрат 3 × 3 в общем виде

x 1 y 1 z 1

x 2 y 2 z 2

x 3 y 3 z 3

и выясним, какими могут быть эти девять чисел.

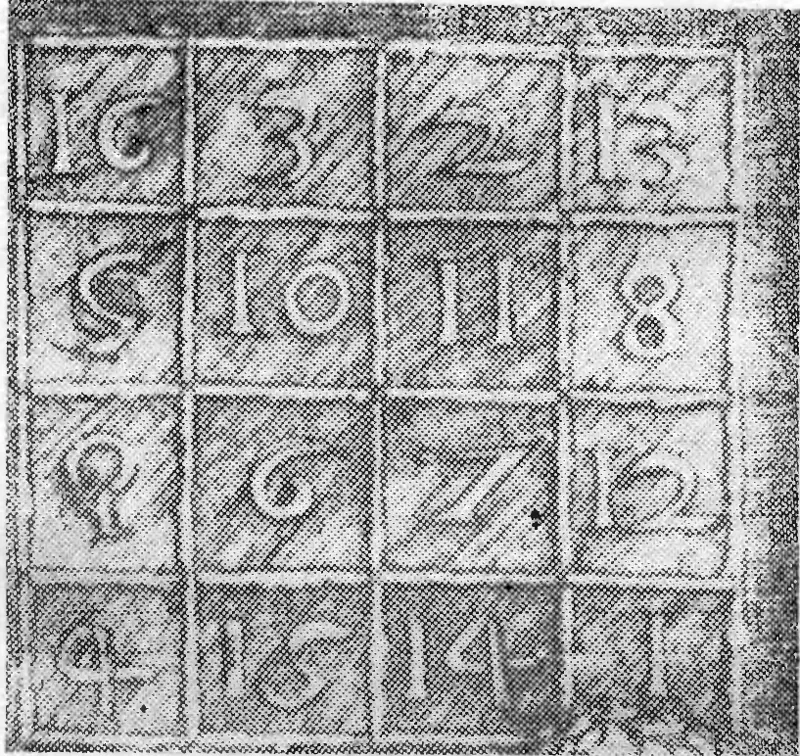
Рис. 9.

Вначале покажем, что центральное число y 2должно равняться 5. Из формулы (1.5.1) следует, что при n = 3 магическая сумма s равна 15. Просуммируем теперь числа во второй строке, втором столбце и обеих диагоналях. В эту сумму каждое число, кроме числа y 2, входит по одному разу; число у 2входит четыре раза, так как оно содержится в каждой из четырех сумм. Поэтому, так как каждая сумма равна s, то

4s = 4 × 15 = 60 =

= x 2+ y 2+ z 2+ y 1+ y 2+ y 3+ x 1+ у 2+ z 3+ z 1+ y 2+ x 3 = З y 2+ x 1+ x 2+ x 3+ y 1+ y 2+ y 3+ z 1+ z 2+ z 3=

= 3 y 2+ 1 + 2 +… + 9 = 3 y 2+ 45.

Следовательно,

З y 2= 60–45 = 15 и y 2= 5.

В таблице

x 1 y 1 z 1

x 2 5 z 2

x 3 y 3 z 3

число 9 не может стоять в углу, так как, если, например, x 1= 9, то z 3= 1 (потому что s = 15), т. е. мы получили бы таблицу

9 y 1 z 1

x 2 5 z 2

x 3 y 3 1

Каждое из четырех чисел y 1, z 1, x 2, х 3должно быть меньше шести, так как y 1+ z 1= х 2+ х 3= 6. Но у нас осталось лишь три числа, меньших шести, а именно: 2, 3 и 4. Таким образом, получилось противоречие. Отсюда мы делаем вывод, что число 9 должно находиться в середине строки или столбца, поэтому наш квадрат может быть записан так:

x 1 9 z 1

x 2 5 z 2

x 3 1 z 3

Число 7 не может быть в одной и той же строке с числом 9, так как тогда сумма чисел в этой строке была бы больше пятнадцати; точно так же число 7 не может быть в одной и той же строке с числом 1, так как тогда оставшееся в этой строке число должно было бы быть также семеркой. Таким образом, 7 не может находиться в углу, и мы можем считать, что наш квадрат имеет следующий вид:

x 1 9 z 1

7 5 z 2

x 3 1 z 3

Числа, находящиеся в одной строке с числом 9 — это 2 и 4, так как иначе сумма в этой строке была бы больше пятнадцати. Далее, число 2 должно быть в том же столбце, что и число 7, так как если бы там стояло 4, то третье число в этом столбце было бы тоже 4. Используя это наблюдение, мы можем определить место каждого из двух оставшихся чисел 6 и 8, в результате получаем магический квадрат, изображенный на рис. 7.

Для б ольших значений n можно построить великое множество магических квадратов. В XVI и XVII веках, и даже позже, составление магических квадратов столь же процветало, как и составление кроссвордов в наши дни. Бенджамин Франклин [2] Бенджамин Франклин (1706–1790) — выдающийся американский общественный деятель, дипломат и ученый. ( Прим. перев .) был страстным любителем магических квадратов. Он позже признавался, что, будучи служащим Законодательного Собрания штата Пенсильвания, он скрашивал скучные часы на службе составлением причудливых магических квадратов и даже магических кругов, в которых числа «стоят на переплетающихся окружностях, причем сумма чисел на каждой из окружностей одна и та же. Следующий эпизод взят нами из Собрания сочинений Бенджамина Франклина [3] The Papers of Benjamin Franclin, Yale University Press, т. 4, c. 392–402. .