Мартин Гарднер - Математические чудеса и тайны

Между прочим, коэффициенты 2, 3, 5 — не наименьшие из возможных в этом фокусе. Можно было бы использовать с тем же успехом, например, коэффициенты 1, 3, 4 ( Асовсем не берет спичек, Бберет дважды столько, сколько у него на руках, В— трижды столько); при этом все суммы не превосходят 19, т. е. можно ограничиться 19 спичками.

Счет заканчивается на той монете, которая окажется последней, если ножку девятки монета за монетой накладывать на кольцо по часовой стрелке, начиная от монеты, следующей (по часовой стрелке) за той, к которой подходит ножка.

Общее число шашек, стоящих в четных вертикальных рядах, изменяется (в ту или иную сторону) ровно на 1 при каждом ходе. При четном числе ходов четность этого числа не изменится и останется такой же, как при первоначальном размещении шашек. Для размещения AAAэто число нечетно, а для размещения ВВВоно четно.

Ниже приводим 8 таких карточек:

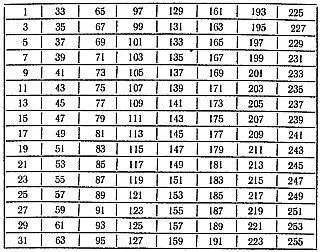
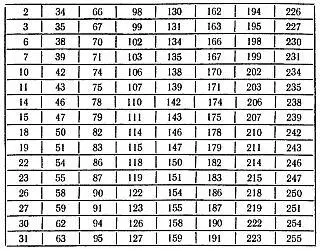
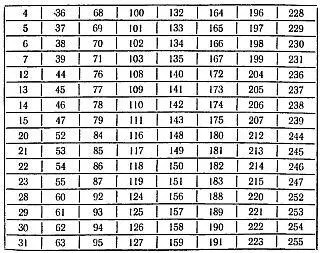
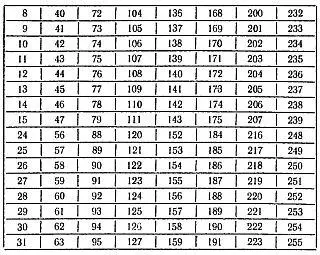
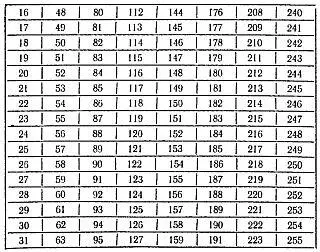
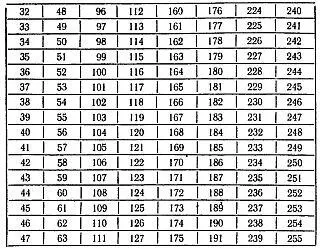
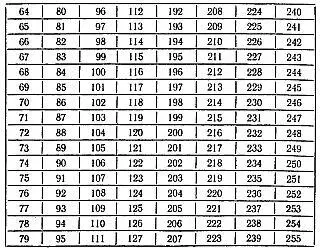
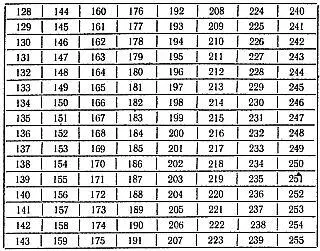
Можно предложить также следующую систему раскраски пластинок и нанесения чисел:

Сумма тонких цифр равна 15, а разность между жирной цифрой и тонкой на каждой фишке есть 5. Поэтому если в начале опыта было k фишек с жирными цифрами, то общая сумма всех цифр, открытых зрителям, была равна 15 + 5k . Допустим, что зритель перевернул i фишек с жирными цифрами и j — с тонкими. Показывающий просит перевернуть обратно эти i фишек и еще k — i фишек, остающихся с жирными цифрами, в итоге общая сумма будет

15 + 5 k + 5 j — 5( k — i ) = 15 + 5( i + j ) = 30,

причем число фишек с жирными цифрами оказывается равным i + j = 3. Пусть, далее, зритель переворачивает и закрывает р фишек с жирными и q с тонкими цифрами. В результате общая сумма цифр на шести фишках станет

30 — 5p + 5q = 30 — 5 p + 5(3 — p ) = 45–10 p = 10(3 — p )+15,

что и дает схему вычислений автора.

Можно упростить счет, если не заставлять зрителя перевертывать накрываемые фишки; тогда сумма цифр накрытых фишек получится вычитанием из 30 суммы цифр открытых фишек.

То же требование о нетрнвнальности следует отнести и к проблеме о разрезании криволинейных плоских фигур. Ясно, что если разрезание и составление по-новому допускает квадрат, то допускает разрезание и составление также плоская фигура с любой границей, содержащая данный квадрат внутри себя.

Ряд, аналогичный ряду Фибоначчи, но начинающийся не с 1 и 1, а с любых чисел а и Ь , имеет вид

а, Ь, a + b, a +2b, 2a + 3b, За + 5b, 5а + 8Ь, 8a + 13b, 13a + 21b, 21a + 34b…

Его коэффициенты суть числа Фибоначчи, а сумма выписанных десяти членов равна, как легко сосчитать, 55 a + 88 b — на одно Ь меньше, чем второе из следующих за написанными чисел ряда.

Если N 0 — год рождения, N 1 — год выдающегося события, a N 2 — текущий год, то мы получает сразу

N 0+ N 1 + (N 2- N 0) + (N 2— N 1) = 2N 2 ,

что и требуется.

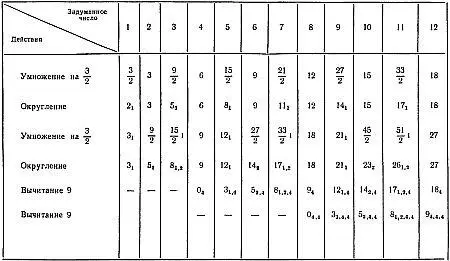
На стр. 123 приведена схема действий в этом фокусе.

Индексы 1, 2, 3, 4 означают ключевые числа, которые запоминает показывающий. Из схемы видно, что задуманное число есть сумма получающихся к концу процесса ключевых чисел. Интересно, что количество чисел, которые можно задумать, можно увеличить. Так, для числа 11 схема остается без изменения, для 12 придется еще раз вычесть 9, что даст третью четверку, и т. д.